【2024《易經》讀經班】招生(雲端課程)
2024年 3 月 9日開始,每周六上午 9:30 ~ 12:00(遇台灣連續假期則停課)
每期約 3 個月左右,至少八堂課,平均約10-12堂課 。 6000元/1期。 (共九期)
上下經全部讀完大約兩年半時間。
雲端課程皆有錄影,如無法到課可觀看影片自行複習。如不克參加,也可購買上一期讀經班的影片。
2024年 3 月 9日開始,每周六上午 9:30 ~ 12:00(遇台灣連續假期則停課)
每期約 3 個月左右,至少八堂課,平均約10-12堂課 。 6000元/1期。 (共九期)
上下經全部讀完大約兩年半時間。
雲端課程皆有錄影,如無法到課可觀看影片自行複習。如不克參加,也可購買上一期讀經班的影片。
《周易古占筮法》是易學網提供給習易者的《易經》讀本,撰寫時間大概在十年前。回顧這本書的內容,有很多個別的資料與看法,現在的我或者已經不認同,或者覺得有錯,另外也有很多不夠成熟或不夠到位的見解。
大家如果對於這本書的改寫有任何想法,或者原本的《周易古占筮法》有什麼該改進與補充的,都歡迎告訴我。
 谷川順比高島吞象早約一甲子,其易學著作除了《左國易一家言》,還有《醫易本義》、《周易本筮指南》、《易學階梯附言》。
谷川順比高島吞象早約一甲子,其易學著作除了《左國易一家言》,還有《醫易本義》、《周易本筮指南》、《易學階梯附言》。
《左國易》基本上就是以《左傳》、《國語》所記載的春秋占例為素材,我們常說的「太卜遺法」,就是周朝卜官、史官實際占卦所用的古法,都是左國的這些卦例為基準的。要了解周朝的太卜遺法,這是最重要的必讀資料。

這本袖珍本《梅花心易》,是我剛從日本古書市場挖寶買回來的古本梅花易。根據的是明朝景泰五年(1454)版本的單卷本。估計印刷時間已超過 350年。目前該版在網路上還找不到其他存在的蹤跡。
未來這個版是否要複刻,我還在考慮之中。易友們也可給我意見。
 作者原本是理工人,從事的是資訓管理工作。在退休之前,就懷抱著對於易學以及先秦思想的興趣,重回校園拿取哲學博士學位,開啟他在人文領域的學術生涯。
作者原本是理工人,從事的是資訓管理工作。在退休之前,就懷抱著對於易學以及先秦思想的興趣,重回校園拿取哲學博士學位,開啟他在人文領域的學術生涯。
《理性讀周易:古經篇》這本書,書名就表明了作者的易學特色與期待:理性的論述。實際閱讀,全書內容也頗為符合這樣的宣言。而「古經篇」也表明了,此書要回歸到「古經」,亦即卦爻辭,來談《周易》,不涉及《彖》、《象》、《文言》等易傳。
 用道家哲學思想來詮釋《周易》,也是陳鼓應老師的最大特色。在此之前,除了一些散置於各處的文章之外,較為系統的易學著作是前一本與趙建偉合寫的《周易注譯與研究》。這本書我在先前的書單推薦裡也提過。
用道家哲學思想來詮釋《周易》,也是陳鼓應老師的最大特色。在此之前,除了一些散置於各處的文章之外,較為系統的易學著作是前一本與趙建偉合寫的《周易注譯與研究》。這本書我在先前的書單推薦裡也提過。
這本《易經導讀及譯註》則是與寇方墀所合著。在翻譯與註解上,此書大量採納當代出土資料的研究成果。難能可貴的是,具學術深度的同時,內容不流於長篇大論,資料堆疊,行文相當簡單明瞭,很適合一般人的閱讀。
此為《繫辭傳》最後一章,孔穎達編為《繫下》第九章。從乾坤的易簡德行開始,緊扣人性之分析,以闡述《周易》的吉凶變化法則。
王弼《周易略例》中採用了該章的許多文字與概念,特別是「情偽」之說,例如〈明爻通變〉開宗明義就說:「夫爻者何也?言乎變者也。變者何也?情偽之所為也。夫情偽之動,非數之所求也。」
此章談易道之興起,以及《周易》作者的時代背景。這也是將《周易》作者指向周文王的最早文獻證據之一。所以鄭玄說:「據此言以易文王所作,斷可知矣。」
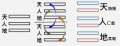 此章從天地人三才的觀點解析六爻的生成原理,以及吉凶原因。像是在為前一章〈原始要終〉的六爻時位提供理論基礎。
此章從天地人三才的觀點解析六爻的生成原理,以及吉凶原因。像是在為前一章〈原始要終〉的六爻時位提供理論基礎。
三才在《繫辭上》第二章又稱三極:「六爻之動,三極之道也。」《說卦傳》則稱三材。天地人三才分別在各自的位置上分出陰與陽,以初與二為地,五與上為天,三與四為人,因此而有了六爻。《說卦傳》所說的:「立天之道曰陰與陽,立地之道曰柔與剛,立人之道曰仁與義。」
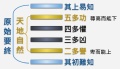 乾卦《彖傳》說:「六位時成」,六爻所居的位置,都有他的「時」。這個「時」是什麼?《繫辭》原始要終章的論述,可謂經典中的經典。習易者若要了解六爻的陰陽變化與時位關聯,一定要研讀透徹。
乾卦《彖傳》說:「六位時成」,六爻所居的位置,都有他的「時」。這個「時」是什麼?《繫辭》原始要終章的論述,可謂經典中的經典。習易者若要了解六爻的陰陽變化與時位關聯,一定要研讀透徹。
依此章,六爻中,上下為初始本末,其初難知,多擬議之辭。上為末為終,其上易知,卒成之終。二與五皆有中庸之德,二謙卑在下而多譽,五尊貴在上居於天子之位而多功。三在下卦之極而多凶,四在外卦之下而多懼。