清華簡《筮法》數字卦解密

 

感謝聖甲蟲學院白中道博士專文介紹本套筮法（有本文的英譯）：

A Theory of the Qinghuajian (V.4) Divination Method

　為推展清華簡筮法的研究與應用，站長已為本文所重建的筮法發明更為簡變的太極丸起卦法。

　起卦程式上線。易學網依照清華簡《筮法》竹簡的數字變化模式，與可能的機率分布，設計一個可以模擬其結果的起卦程式。

近來沉浸在清華簡《筮法》的研究，只差臨門一腳就可以將這個（可能是）傳說中古老的「歸藏易」占法與筮法重建起來。

這臨門一腳是關於「筮法」的部份，也就是卦應該如何算出來的基本問題：本文就是要挑戰這個不可能的任務。

竹簡中所談占法，也就是怎麼看出卦象吉凶的方法，雖然還有許多細節不甚清楚，但是基礎框架與原理都有個輪廓，要拿這套占法來應用至少有理可循了，或許只是實際應用的問題，假以時日應該就會越來越清楚。但筮法方面卻沒有任何文字說明，只有57個卦例讓你摸索。

↓　這是57組卦例中的30組，這些數字之間有怎麼樣的變化關係？是怎麼算出來的？

清華簡這57組卦都是每組一對的兩個卦，每個卦都是由六個數字所組成。這些卦是否像《周易》一樣是算出一卦並依「爻變」再畫出「之卦」？如果是，那麼到底左為本卦還是右為本卦？如果不是，那麼是先算右卦，還是先算左卦？其次，四、五、六、一（七）、八、九這些筮數到底是怎麼算出來的？如何記錄為卦象？

由於清華簡內容幾乎全都屬於占法原則的說明，類似於我們現在教人如何解讀卦象的書，並非實際的卦例，因此無法從這57組卦例研究出關於每個筮數的「機率」，但是我們可以從中研究出一些諸如筮數間可能如何互變的基本資料。

更精確的來說，裡面其實有一組卦可能是實際揲蓍而成的解卦卦例，但由於卦例太少，也無法從中統計出任何有意義的實揲機率。

為了求證，我們將這57組卦的筮數整理為表，共得342組筮數（如後表）。然後依各種可能的假設前題來做統計計算，最後基於「左為本卦，右為之卦」的假設的確找到「有理可循」的數字變化關係，因此可推斷左邊為「本卦」，右邊為類似於「變卦」或「之卦」的衍生卦。

因此我們可以確定清華簡的卦應該是只求出6個筮數，再以這6個原始筮數畫為兩卦，而且是先畫左卦，再畫右卦。換句話說，其畫卦的方向洽與文字閱讀方向相反，並不是由右而左，這可能與《周易》筮法的做法是一致的。至於算卦過程是由下爻往上算，還是由上往下？依理來推論，應該是由下往上。其一、周易如此。其二，其畫卦的左右向是與文字書寫、閱讀方向相反，因此爻的畫法也可能如此，是與書寫及閱讀方向（由上往下）相反，也就是由下往上。

↓　從後面的數字表格，可以整理出這樣的數字變化關係。

四	五	六	一（七）	八	九
4→4　x2 4→6　x1 4→1　x2	5→5　x4 5→6　x3 5→1　x2	6→6　x68 6→1　x88	1→1　x62 1→6　x89	8→8　x2 8→6　x2 8→9　x4	9→9　x6 9→6　x4 9→1　x3

按：清華簡中，筮數「一」代表的是「七」，因此一即是七，七即是一。［4→4 x2］出現2次的左四右四；［4→6 x1］ 出現1次的左四右六。其餘以此類推。

從上表我們可以看到這些筮數間的變化法則大致如此：

• 六和一（七）兩個筮數之間可以互變，但不會變成其餘四個筮數。
• 四、五、八、九等四個筮數都可以變成兩個筮數，但八的變法和四、五、九不一樣。
• 四、五、九三個筮數可變為六和一。
• 八可變為六和九。八不變成一，而變成九，這是比較特殊而奇怪的。是否其中有什麼錯誤？照理來推測，應當與其他筮數一樣變為六、一才是。這當中原因，還有待更多出土資料來證明。本文謹就目前可得資料暫作合理推論。

一 1-1 1-1 6-1 1-1 6-1 1-1 ──

二 1-1 6-6 1-6 6-1 6-1 1-1 ──

三 6-6 1-6 6-1 6-6 1-1 1-6 ──

四 1-6 6-1 1-1 6-6 6-1 1-1 ──

五 6-6 1-6 6-1 6-6 5-1 9-6 ──

六 1-6 6-1 1-1 9-6 5-1 6-1 ──

七 1-6 1-6 6-1 1-6 6-6 1-6 ──

八 1-1 1-6 1-6 1-6 6-6 6-6 ──

九 1-6 6-1 1-6 6-6 1-6 1-1 ──

十 6-1 6-1 6-1 1-6 1-6 6-6 ──

1-1 1-6 6-1 6-1 6-6 6-6 ──

6-6 1-6 1-6 1-6 6-1 1-1 ──

6-6 6-1 1-6 9-6 1-6 6-1 ──

6-6 1-6 1-6 1-1 1-6 1-1 ──

4-6 5-6 9-1 1-6 1-1 6-6 ──

6-6 6-1 6-1 6-1 1-1 1-1 ──

1-1 1-1 6-1 8-6 1-6 1-6 ──

6-6 1-6 1-1 1-1 6-1 5-6 ──

6-6 1-1 1-6 9-1 1-6 6-1 ──

1-1 6-6 1-6 1-6 1-1 4-1 ──

6-6 6-6 6-6 1-6 1-6 6-6 ──

1-1 1-1 1-1 1-1 6-1 6-1 ──

6-6 6-1 6-1 6-1 6-1 6-1 ──

1-1 1-6 1-6 6-6 1-6 1-6 ──

6-6 1-6 6-1 6-1 1-6 1-1 ──

1-1 1-6 1-6 6-1 6-1 6-6 ──

1-6 6-6 1-6 6-1 1-6 1-6 ──

6-1 1-6 6-6 1-1 1-1 6-1 ──

6-1 1-6 1-6 6-1 6-1 1-1 ──

9-1 8-6 1-6 1-1 6-1 6-1 ──

1-6 1-6 6-6 6-1 1-1 6-6 ──

1-6 6-6 6-1 1-1 6-1 1-1 ──

1-1 6-6 1-6 6-1 6-1 6-1 ──

1-1 6-1 1-6 6-1 6-1 6-1 ──

1-6 1-1 6-1 1-1 1-6 1-6 ──

6-6 6-1 6-1 6-1 1-6 6-6 ──

1-6 1-1 6-1 6-1 1-6 6-6 ──

1-6 1-6 6-6 1-1 6-6 1-6 ──

6-6 6-1 6-1 1-1 6-1 6-1 ──

9-9 1-1 1-1 9-9 6-1 6-1 ──

9-9 1-1 1-1 8-9 6-1 6-1 ──

8-9 6-1 1-1 8-9 6-1 6-1 ──

9-9 6-1 6-1 8-9 6-1 6-1 ──

6-6 6-6 6-6 1-6 1-6 6-6 ──

6-6 6-6 6-6 1-6 6-6 1-6 ──

6-6 6-6 6-6 6-6 1-6 1-6 ──

6-6 6-6 6-6 9-6 6-6 6-6 ──

1-6 6-1 1-6 6-1 1-6 1-1 ──

1-6 6-1 1-6 1-1 1-6 6-1 ──

6-6 6-6 1-1 6-6 5-6 4-1 ──

1-6 1-6 6-6 6-1 6-1 1-1 ──

4-4 5-5 6-6 1-1 8-8 9-9 ──

9-9 8-8 1-1 6-6 5-5 4-4 ──

1-6 1-1 5-5 5-5 6-6 1-6 ──

6-6 6-1 1-6 6-1 1-6 1-1 ──

1-6 6-6 1-6 6-1 6-6 1-6 ──

6-1 1-1 6-1 1-6 1-1 6-1 ──

──

──

──

至於筮數何時該變，何時不該變？

在毫無頭緒下，我們只能先做各種假設來逐一驗證其可能性。

我們以過去張政烺對數字卦的研究統計大概可知，最早的筮數可能有一至八，未見到的二、三則可能被歸到六和七。因此我們也可假設清華簡筮法中或許也應當有八個或九個筮數，未出現的兩個推理為二、三，或者再加上一（注意，清華簡中一這個符號是被當作七用）。或許當筮數出現六、七時，就不變，記為六→六，一→一。而若是二、三時，則分別記為六→一，及一→六。一可能記作一→六。但其他筮數呢？所以依這個假設顯然是行不通的。

或者假設筮數並不是八個，就是簡上看到的四、五、六、七（一）、八、九這六個，那麼一與六何時互變？何時不變？或許答案與四、五、八、九其餘四個筮數何時當變何時不當變的法則也是相關或連動的，甚至是一樣的。

但四、五、八、九這四個筮數的變與不變的原則看來也有些複雜。因為當它變時，並不是只變某一特定的數而已，而是可能變成兩個。

筆著曾經懷疑，是否與春夏秋冬有關？但顯然這是無法成立的。例如在〈節戰〉一節中「內勝外」（筮數由上至下為四五六一八九）及「外勝內」（九八一六五四）的卦象中，六個筮數同時出現，而且全部未變。但在第二節〈得〉「見丁數」的卦例中 （由上至下分別為四五九一一六、六六一六一六）則是四、五、九皆變：四變六、五變六，九變一。這兩組卦例直接就可否決了數字依季節而決定變或不變的假設。因為四五九確定分屬不同季節的筮數，如果是依季節而變，那麼這兩個例子裡一次只能一個或兩個爻變（清華簡將春夏視為同一季節，秋冬亦然），無法讓這三個筮數同時變。且如果是以季節來決定，那麼六個筮數同時出現時，理當至少有一筮數變，或者是兩個筮數。

基於類似的理由，連帶的，以干支來決定變或不變的假設，也可以直接排除在外。

逆向工程

以上是筆者在逆向工程之前做過的其他可能假設與推理、試算，但多數是可輕易印證無效而排除在外的猜測，也歷經各種嘗試皆徒勞無功。

最後只能假設一個可能：筮數的變與不變，應當決定於揲蓍過程中的某個結果。

可是清華簡未留下任何關於筮法的隻字片語，關於如何揲蓍算卦可說毫無頭緒。

因此我再做一個大膽猜測：是否可從《周易》筮法來修改？

這其中道理是這樣的：其一，清華簡第三十節〈十七命〉說：「凡是，各當其刲，乃力占之。占之必力，刲乃不忒。」意思大概是說，占筮一定要經過「掛扐」，也就是揲蓍起卦的程序，這樣占筮才會準。力通扐，指的可能是揲蓍的掛扐。

其二，清華簡的占法與《周易》有一個相當清楚的演化關係，清華簡像是早於周易並保留更早數字占的筮法，而周易則像是清華簡筮法的簡化、抽象化演進。具體來說，《周易》把數字的爻象與卦象融合於八卦卦象，將六個筮數減少為四個筮數，進而精簡為只有陰陽，因此從某種程度來說，周易可視為是歸藏的簡化。那麼，相對應的，我們可以推想，或許其揲蓍法也存在著這樣的關聯，方法及過程都與今存周易的揲蓍法有些類似，差別只在於這個方法要求出六個筮數，而且這六個筮數存在著上表所列的變化關係。而且由於六個筮數較四個更多，因此其程序是較為複雜的。

逆向工程到這裡，我們總算有個頭緒，但問題是要從多少枚蓍策開始？50？還是其他數字？這讓我想起《繫辭傳》的「大衍」章：

大衍之數五十，其用四十有九，分而為二以象兩，掛一以象三，揲之以四以象四時，歸奇於扐以象閏，五歲再閏，故再扐而後掛。天數五，地數五，五位相得而各有合。天數二十有五，地數三十，凡天地之數，五十有五，此所以成變化，而行鬼神也。

兩千年來，「大衍之數五十」和「天地之數五十有五」這兩個數不知耗盡了多少中國儒生的精力與研究，這兩個數字偃然是易學上的一個灘頭堡，易學家們總得五、十、十五像在喊數字拳一樣用盡心思解釋這兩個數字背後的哲學思想，以建立其易學地位。不過筆者對於儒生們的數字拳沒有興趣，引起我興趣的是「五十五」這個數字的實用價值。

「五十」這個數是有其揲蓍實用意義的，但五十五呢？我大膽猜測這是《周易》之前，也就是清華簡所用的蓍策數。那麼，這個蓍策數能不能依「大衍」揲蓍法的類似方法算出四、五、六、七、八、九這六個筮數，並內含一個簡單而合理的筮數變化法則呢？

答案是肯定的！我略微盤算之後，覺得很有可能，於是實際的設計出一個類似於《周易》的揲蓍法，而且能夠重現這些筮數。而在實際操作演練數日之後，也證明可行！

清華簡《筮法》揲蓍法重建

由於揲蓍法的操作相當繁鎖，這裡只談一些與傳統揲蓍法的重大差異之處，以及結果如何解讀等問題，共通的操作法還是參閱以下兩篇文章：

• 易經卜卦的原點：大衍之數揲卦法
• 詳談揲蓍法（或稱「筮法」，「大衍揲卦法」）

《周易》的揲蓍法每爻有3變，清華簡的筮法我們姑且稱它為《歸藏易》（但這還有待證實），則每爻5變，除了第一變，其餘四變大致可遵照「分二、掛一、揲四、歸奇」的步驟，但如何「歸奇」的方法有所不同。

1.  第一變：直接以55枚蓍策開始，不用掛一，也不需「其一不用」。然後分二，揲四，最後將兩邊餘策（可能有1-2、2-1、3-4、4-3四種組合）全部夾於指間。最後夾於指間可能為三策，可能為七策。（如下圖，總共掛了七策。）

2.  第二至五變：依分二、掛一、揲四、歸奇操作。但這裡的歸奇和《周易》不一樣，必需分兩邊歸奇。左邊的餘策放左上方，右邊的餘策歸於右上方，左右分別置放。（如圖）掛一與先前的掛三或七交叉分開。

3. 五變成爻：依第二變方法再繼續操作三、四、五變。由於二、三、四、五變都掛一，因此見手上除了第一變時的餘策之外，累積「掛四」時，就是成一爻。這時將筮數記下。如圖，「掛一」的指間策數到四枚時，就知已經成爻。這時準備記錄筮數，關於筮數如何記錄，請看後面說明。

4. 記錄本卦筮數：此時計算桌上的蓍策數，四枚一堆，共有幾堆，筮數就記多少。筮數記錄法如下圖，由左至右分別為四、五、六、七、八、九

 

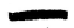
5. 記錄變卦筮數：以上筮數為本卦中的筮數。接下來分別計算左上和右上蓍策的「歸奇」數。若兩邊蓍策數相同，則筮數不變，變卦中的筮數與本卦中一致。（如下圖，過揲之策數總計有六堆，所得筮數為六，後面餘策左右皆十，故此爻不變，變卦中筮數仍為六。）

如果左右兩邊筮數不一致，六與一兩數互變。六變一，一變六。但四、五、八、九筮數若右邊大則筮數變一或九，若右邊小則筮數變六。具體而言，六個筮數的變化如下：

• 四 →右小則變六，右大變為一
• 五→右小則變六，右大變為一
• 六→無論大小，一律變為一。
• 七→無論大小，一律變為六。
• 八→右小則變六，右大變為九
• 九→右小則變六，右大變為一

6. 六爻成卦：重覆以上操作六次，共得六組筮數，完成一卦。注意的是，筮數應該從左向右，由下往上畫。

我們以實際操作得到的結果為例，記錄如下：

所得筮數	左-右歸奇策數	變爻
第六爻：八 第五爻：五 第四爻：七 第三爻：七 第二爻：六 第一爻：六	9-7 14-14 11-9 8-12 13-11 10-10	六 五 六 六 七 六

另外再筮兩卦，如下：

第六爻：六 第五爻：六 第四爻：九 第三爻：五 第二爻：七 第一爻：五

10-14 9-11 5-7 11-13 8-8 12-12

七 七 七 七 七 五

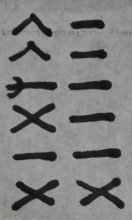第六爻：五 第五爻：六 第四爻：五 第三爻：六 第二爻：六 第一爻：六

14-14 13-11 11-13 11-13 13-11 11-9

五 七 七 七 七 七

在決定爻變的因子時，筆者曾想過是否以第一變中所掛的策數大小來控制？因為第一變中可能掛3策或7策。但發現這行不通，因為筮數四的情況下第一變一定是掛7，若是筮數九則一定是掛3，就無法有變化。

以上這個方法，不但能夠成功算得清華簡中的卦象，且都符合清華簡中所呈現出的數字間的變化關係，且從各種角度來看都相當合理，不論是從機率分配的合理性，還有其變化的機制。且每個環節都能夠從古典中找到依據。因此個人相信，這應當會有點像古法。

至於以上卦象該如何實際利用清華簡中的法則來解釋吉凶，這個還有待我們慢慢揣摩與練習、嘗試了。