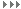閱讀古書, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56>, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126
啓蒙附論
朱子之作《啓蒙》，蓋因以象數言易者，多穿穴而不根，支離而無據。然易之為書，實以象數而作，又不可略焉而不講也。且在當日，言圖書卦畫蓍數者，皆創為異論，以毀成法。師其獨智，而訾先賢，故朱子述此篇以授學者，以為欲知易之所以作者，於此可得其門戶矣。今摭圖書卦畫蓍數之所包蘊，其錯綜變化之妙，足以發朱子未盡之意者凡數端，各為圖表而繫之以說，蓋所以見圖書為天地之文章，立卦生蓍為聖神之製作，萬理於是乎根本，萬法於是乎權輿，斷非人力私智之所能參，而世之紛紛撰擬，屑屑疑辨，皆可以熄矣。
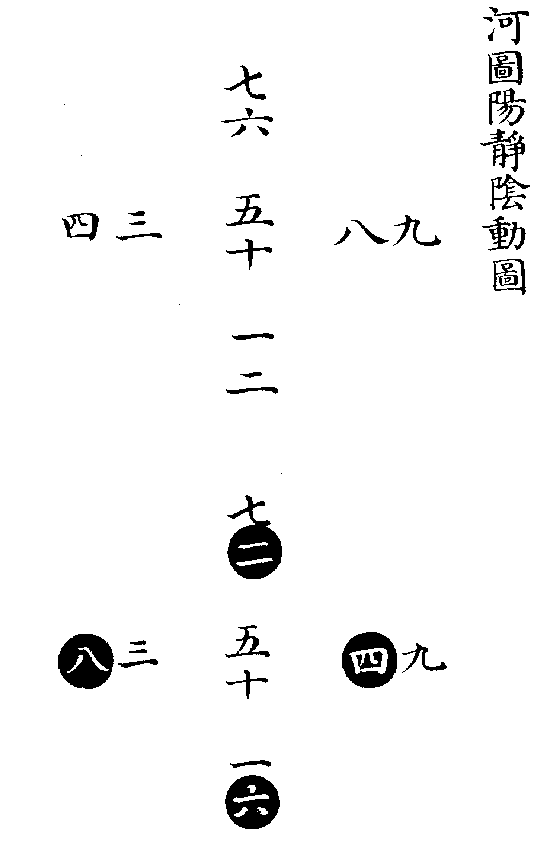
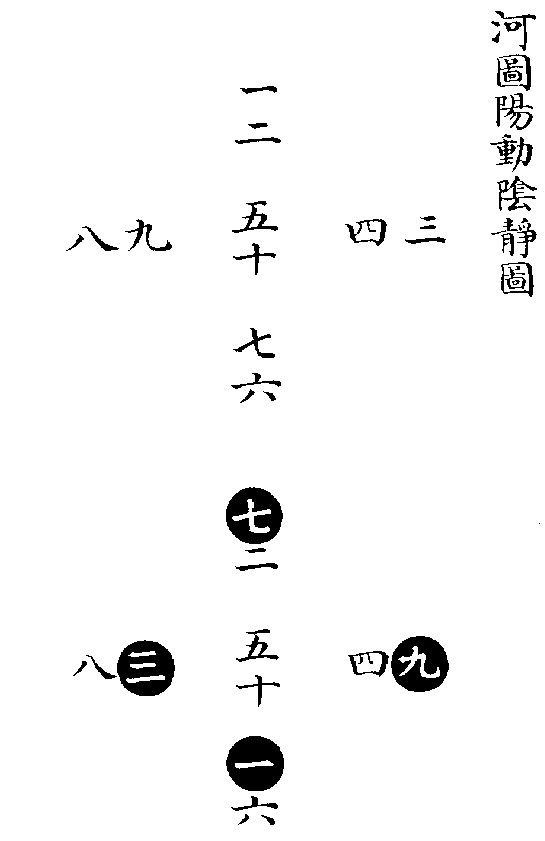
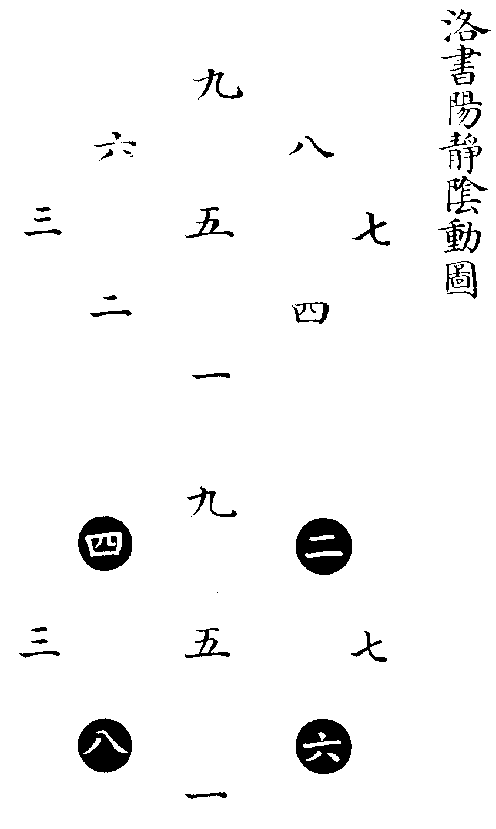
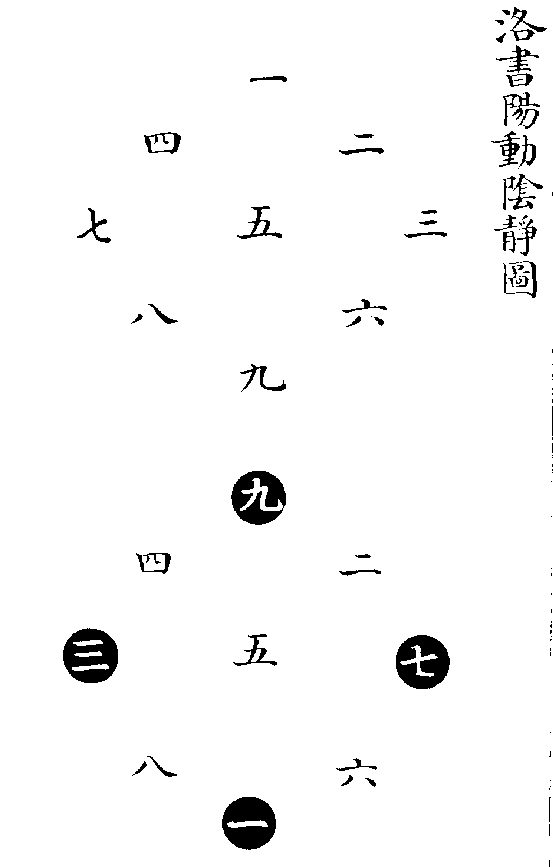
《大傳》言《河圖》，曰一二，曰三四，曰五六，曰七八，曰九十，則是以兩相從也。《大戴禮》言《洛書》，曰二九四，曰七五三，曰六一八，則是以三相從也。是故原《河圖》之初，則有一便有二，有三便有四，至五而居中；有六便有七，有八便有九，至十而又居中，順而布之，以成五位者也。原《洛書》之初，則有一二三，便有四五六。有四五六，便有七八九。層而列之，以成四方者也。若以陽動陰靜而論，則數起於上。故《河圖》之一二本在上也，三四本在右也，六七本在下也，八九本在左也。《洛書》之一二三，四五六，七八九，本自上而下也。於是陽數動而交易，陰數靜而不遷，則成《河圖》、《洛書》之位矣。如以陽靜陰動而論，則數起於下。故《河圖》之一二本在下也，三四本在左也，六七本在上也，八九本在右也。《洛書》之一二三，四五六，七八九，本自下而上也。於是陽數靜而不遷，陰數動而交易，則又成《河圖》、《洛書》之位矣。蓋其以兩相從者，如有天則有地也，有君則有臣也，有夫則有婦也。以三相從者，如有天地則有人也，有君臣則有民也，有父母則有子也。陽動陰静者如乾君而坤藏也，君令而臣從也，夫行而婦順也。自上而下，以用而言者也。陽静陰動者，如乾主而坤役也，君逸而臣勞也，父安居而妻子勤職也。自内而外，以體而言者也。同本相從，以成合一之功。動静相資，以播生成之化。造化人事之妙，窮於此矣，先後天圖象之精藴，莫不於此乎出也。
自《洛書》以三三積數，為數之原，而自四以下，皆以為法焉，何則？三者天數也，故其象圓，如前圖。居四方與居四隅者，或動或靜（居中者一定不易），而各成縱橫皆十五之數矣。四者地數也，故其象方，如後圖。居中居四隅與居四方者，或動或靜，亦各成縱橫皆三十四之數矣。自五五以下，皆以三三圖為根。自六六以下，皆以四四圖為根，而四四圖，又實以三三圖為根。故《洛書》為數之原，不易之論也。今附四四圖如左，以相證明，其餘具數學中，不悉載。
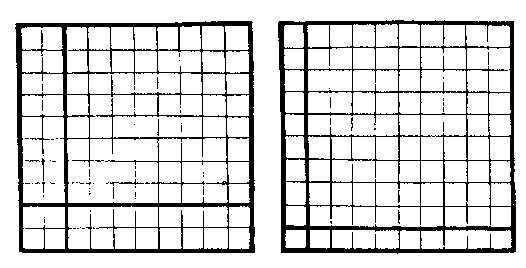
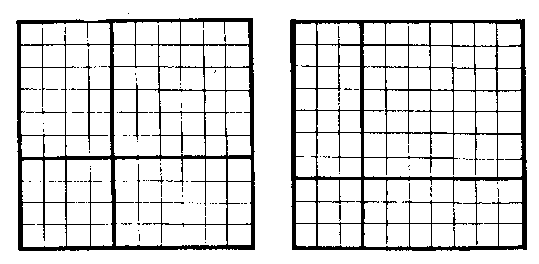
此以十六數自左而右，自上而下列之（第一圖），其居中與居四隅者不易，而居四方者交易，則成縱橫皆三十四之數（第二圖）。若居四方者不易，而居中與居四隅者交易，亦成縱橫皆三十四之數（第三圖）。
此以十六數自右而左，自下而上列之（第一圖），用前法變為兩圖（第二圖，第三圖），並得縱橫皆三十四之數，但其不易者，即前之交易者，而其交易者，即前之不易者（此第二圖同前第三圖，此第三圖同前第二圖），蓋亦陰陽互為動靜之理云。
加減河圖之原
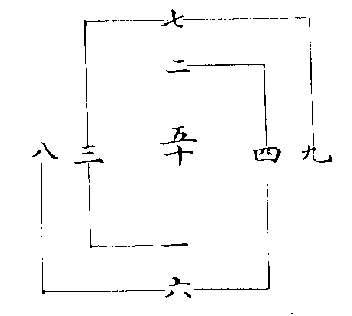
一 三 七 九
用中兩率，三七相加為十，以一減之得九，以九減之得一。
若用一九相加亦為十，以三減之得七，以七減之得三。
二 四 六 八
用中兩率，四六相加為十，以二減之得八，以八減之得二。
若用二八相加亦為十，以四減之得六，以六減之得四。
洛書乘除之原
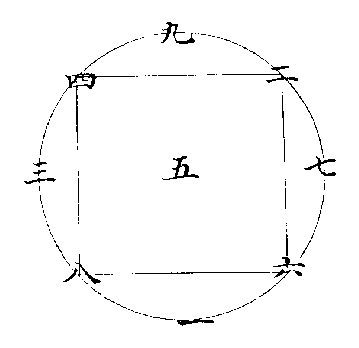
一 三 九 七
用中兩率，三九相乘為二十七，以一除之得二十七，以二十七除之得一。
若用一與二十七相乘，以三除之得九。以九除之得三。
二 四 八 六
用中兩率，四八相乘為三十二，以二除之得十六，以十六除之得二。
若用二與十六相乘，以四除之得八，以八除之得四。
《大傳》曰：「天一地二，天三地四，天五地六，天七地八，天九地十。」天地之數，皆自少而多，多而復還於少，此加減之原也。又曰：「參天兩地而倚數。」天數以三行，地數以二行，此乘除之原也，是故《河圖》以一二為數之體之始，《洛書》以三二為數之用之始。然《洛書》之用，始於參兩者，以參兩為根也，實則諸數循環，互為其根，莫不寓乘除之法焉，而又皆以加減之法為之本。今推得洛書加減之法四，乘除之法十六，積方之法五，句股之法四，各為圖表以明之如左。
洛書加減四法
一用奇數左旋相加，得相連之耦數。
一加三為四，三加九為十二。
九加七為十六，七加一為八。
若用奇數減左旋相連之耦數，得右旋相連之奇數。
三減四為一，九減十二為三。
七減十六為九，一減八為七。
一用耦數左旋相加，得相連之耦數。
二加六為八，六加八為十四。
八加四為十二，四加二為六。
若用耦數減左旋相連之耦數，得右旋相連之耦數。
六減八為二，八減十四為六。
四減十二為八，二減六為四。
一用奇數右旋加耦數，得相連之奇數。
一加六為七，七加二為九。
九加四為十三，三加八為十一。
若用奇數減相連之奇數，得相連之耦數。
一減七為六，七減九為二。
九減十三為四，三減十一為八。
一用耦數右旋加奇數，得相對之奇數。
二加九為十一，四加三為七。
八加一為九，六加七為十三。
若用奇數減相對之奇數，得相連之耦數。
九減十一為二，三減七為四。
一減九為八，七減十三為六。
洛書乘除十六法
一用三左旋乘奇數，得相連之奇數。
三二如九，三九二十七。
三七二十一，三一如三。
一用八左旋乘耦數，得相連之耦數。
八八六十四，八四三十二。
八二一十六，八六四十八。
一用三左旋乘耦數，得相連之耦數。
三四一十二，三二如六。
三六一十八，三八二十四。
一用八左旋乘奇數，得相連之耦數。
八三二十四，八九七十二。
八七五十六，八一如八。
一用二右旋乘耦數，得相連之耦數。
二二如四，二四如八。
二八一十六，二六一十二。
一用七右旋乘奇數，得相連之奇數。
七七四十九，七九六十三。
七三二十一，七一如七。
一用二右旋乘奇數，得隔二位之耦數。
二九一十八，二三如六。
二一如二，二七一十四。
一用七右旋乘耦數，得相連之耦數。
七二一十四，七四二十八。
七八五十六，七六四十二。
一用一乘奇數，得本位之奇數。
一一如一，一三如三。
一九如九，一七如七。
一用六乘耦數，得本位之耦數。
六六三十六，六八四十八。
六四二十四，六二一十二。
一用一乘耦數，得本位之耦數。
一二如二，一四如四。
一八如八，一六如六。
一用六乘奇數，得相連之耦數。
六七四十二，六九五十四。
六三一十八，六一如六。
一用四乘耦數，得相對之耦數。
四四一十六，四六二十四。
四二如八，四八三十二。
一用九乘奇數，得相對之奇數。
九九八十一，九一如九。
九三二十七，幾七六十三。
一用四乘奇數，得隔二位之耦數。
四九三十六，四七二十八。
四一如四，四三一十二。
一用九乘耦數，得相對之耦數。
九二一十八，九八七十二。
九四三十六，九六五十四。
凡除法，除其所得之數，得其所乘之數。
《洛書》乘除十六法，可約為八法，何則？五者河洛之中數，自此以上，由五以生。五加一為六，六減五為一，是六與一同根也。五加二為七，七減五為二，是七與二同根也。三八四九，其理如之。今用三與八左旋乘奇耦而皆得相連之奇耦，可以知八即三矣。用二與七右旋乘奇耦而皆得相連之奇耦，可以知七即二矣。内惟二乘奇數得隔二位之耦數者，其所得即相連奇位同根之數，猶之乎相連也。（如二九一十八，八與三同根，得八猶之得相連之三也。餘倣此。）用一與六乘而皆得本位之奇耦，可以知六即一矣，内惟六乘奇數得相連之耦數者，其所得即本位同根之數。猶之乎本位也。（如六七四十二，七與二同根。得二猶之得本位之七也。餘倣此。）用四與九乘而皆得對位之奇耦，可以知九即四矣，内惟四乘奇數得隔二位之耦數者，其所得即對位同根之數，猶之乎對位也。（如四九三十六，六與一同根。得六猶之得對位之一也。餘倣此。）其但得同根之數者，何凡奇乘耦，耦乘耦所得皆耦數而同。（如三四一十二，八四亦三十二。）奇乘奇，其得數為奇。若耦乘奇，不能得奇數而同，故但得其同根之耦數也。（如三三為九，八三二十四。九與四同根，得四猶之得九也。）所以一六二七三八四九在河圖則四方之相配，在洛書則正隅之相連，以其數之生於中五而同根也。
數有合數，有對數。合數生於五，對數成於十。一六，二七，三八，四九，此合數也，皆相減而為五者也。一九，二八，三七，四六，此對數也，皆相併而為十者也。在《河圖》，則合數同方，而對數相連。在《洛書》，則合數相連，而對數相對。相合之相從者，六從一也，七從二也，八從三也，九從四也（如前乘除十六法）。相對之相從者，九從一也，八從二也，七從三也，六從四也（如後積方五法）。凡以合數共乘一數，所得之數必同（乘耦既同數，乘奇則同報）。若各自乘焉，則又必合矣（如三三得九，八八六十四）。以對數共乘一數，所得之數必對（如三三得九，七三二十一）。若各自乘焉，則又必同矣（如一一得一，九九亦八十一。二二得四，八八亦六十四）。是以自乘之數，相合之相從者，此得自數，則彼亦得自數也（如一得一，六得六）。此得對數則彼亦得對數也（如四得六，九得一）。此得連數，則彼亦得連數也（如三得九，八亦得四。二得四，七亦得九）。相對之相從者，此得自數，則彼得對數也（如一得一，九亦得一。六得六，四亦得六）。此得連數，則彼亦得連數也（如三得九，七亦得九。二得四，八亦得四）。要皆會於一六四九而齊焉。故開平方之自乘數，止於一六四九，而《洛書》之位，一六四九居上下以為經，二七三八、居左右以為緯者，此也。
《洛書》對位成十互乘成百圖
一與九對成十（十自乘其積一百）。
九自乘八十一；一自乘一；一乘九、九乘一，俱為九，共十八；合之一百（與十自乘積同）。
二與八對成十。八自乘六十四；二自乘四；二乘八、八乘二，俱十六，共三十二；合之一百。
三與七對成十。七自乘四十九；三自乘九；三乘七、七乘三，俱二十一，共四十二；合之一百。
四與六對成十。六自乘三十六；四自乘十六；四乘六、六乘四，俱二十四，共四十八；合之一百。
中五含五成十。五自乘二十五；又五自乘二十五；又五互乘各二十五，共五十。合之一百。
洛書句股圖
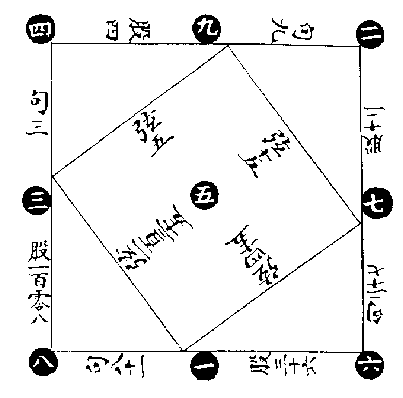
句三，股四，弦五。
句九，股十二，弦十五。
句二十七，股三十六，弦四十五。
句八十一，股一百零八，弦一百三十五。
此《洛書》四隅合中方，而寓四句股之法者，推之至於無窮，法皆視此。
河洛未分未變方圖
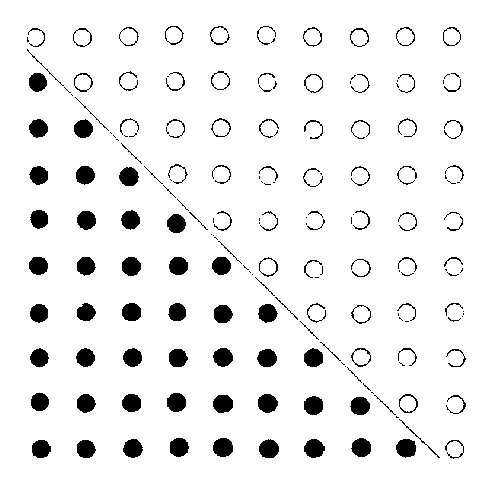
《河圖》之數，五十有五。《洛書》之數，四十有五，合為一百，此天地之全數也。以一百之全數，為斜界而中分之，則自一至十者，積數五十有五，自一至九者，積數四十有五。二者相交，而成河洛數之兩三角形矣。凡積數自少而多，必以三角，而破百數之全方，以為三角，其形不離乎此二者，下諸圖之根，實出於此。
河洛未分未變三角圖
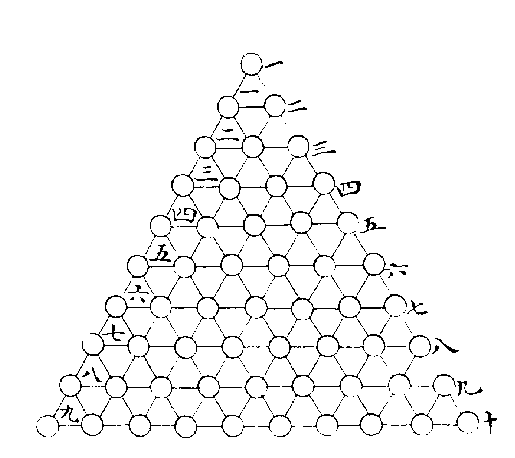
《河圖》之數，自一至十。《洛書》之數，自一至九。象之已分者也。圖則生數居內，成數居外。書則奇數居正，耦數居偏，位之已變者也。如前圖，破全方之百數，以為河洛二數，又就點數十位，中涵冪形之九層，以為河洛合一之數，則雖其象未分，其位未變，而陰陽相包之理，三極互根之道，已粲然默寓於其中矣。故為分析以明之，如後論。
點數應《河圖）十位
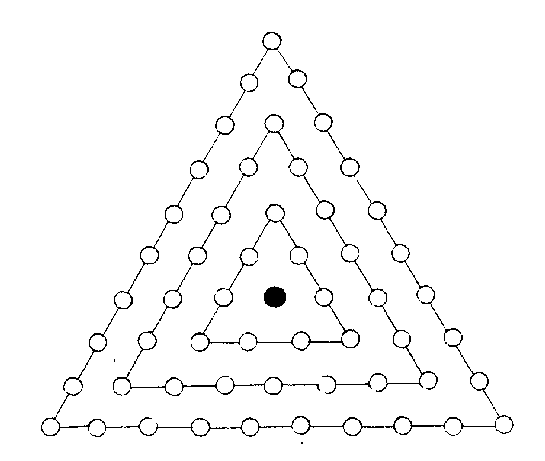
周圍三角，分三重，中一重九，次內一重二九一十八，外一重三九二十七，除中心，凡五十四。
若自上而下作三層，亦如之。
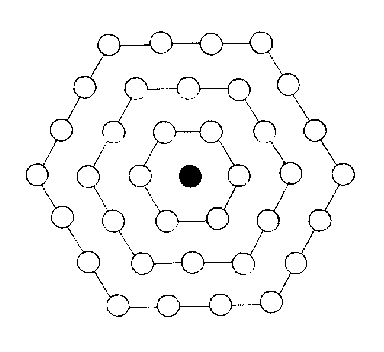
中含六角，亦分三重，中一重六，次內一重二六一十二，外一重三六一十八，除中心，凡三十六。
若自上而下作三層，亦如之。
冪形應《洛書》九位
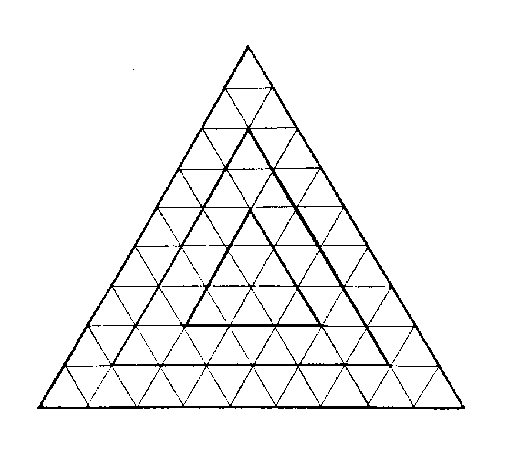
周圍三角分三重，中一重九，次內一重三九二十七，外一重五九四十五，凡八十一。
若自上而下作三層，亦如之。
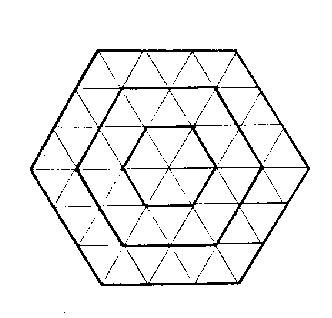
中含六角，亦分三重，中一重六，次內一重三六一十八，外一重五六三十，凡五十四。
若自上而下作三層，亦如之。
以上諸圖，本同一根，雖積數若異，而其為九六之變則一也。九六可分為內外中之三重，亦可分為上下中之三層，就每重每層論之，則九為天而包地，六為地而涵於天，心為人而主乎天地。統三重而論之，則外為天，內為地，而中為人也。統三層而論之，則上為天，下為地，而中為人也。又合而論之，則九六者，在天為陰陽，在地為柔剛，在人為陰陽剛柔之會，而其心則天地人之極也，以上下分者，其心有三，所謂三極之道，三才各具一太極也；以內外分者，其心惟一，所謂人者天地之心，三才經體一太極也。
此圖之中，渾具理象數之妙者如此，故分而為圖，則應乎陰陽剛柔之義，根於極而迭運不窮。聖人則之，易有太極，是生兩儀，陽九陰六，命爻衍策者此也。分而為書，則應乎三才之義，主於人而成位其中，聖人則之。皇極既建，彜倫攸敘，參天貳地，垂範作疇者此也。
或曰：《河圖》、《洛書》，出於兩時，分為兩象，今以一圖括之可乎？曰：十中涵九，故數終於十，而位止於九，此天地自然之紀，而圖書所以相經緯而未嘗相離也。非有十者以為之經，則九之體無以立。非有九者以為之緯，則十之用無以行。不知圖書之本為一者，則亦不知其所以二矣。
或曰：《河圖》、《洛書》，有定位矣，今以為有未變者何與？曰：《易大傳》之言《河圖》也，曰「天一地二，天三地四，天五地六，天七地八，天九地十」，順而數之，此其未變者也。又曰「天數五，地數五，五位相得，而各有合」，分而置之，此其定位者也。如易卦一每生二，以至六十有四，則其未變者也。乾南坤北，離東坎西，則其定位者也。不知未變之根，則亦不足以識定位之妙矣。
冪形為算法之原
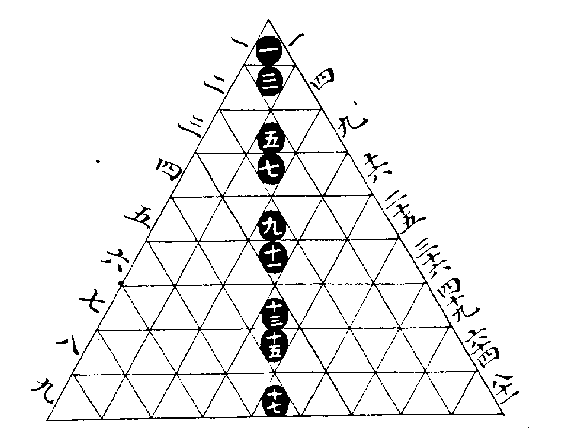
此圖左方注者，本數也，自一至九而用數全矣。中列注者，加數也，一加二為三，二加三為五，至於八加九而為十七，皆以本數遞加，而每層之冪積如之。右方注者，乘數也，一自乘一，其冪積一。二自乘四，其冪積合一三兩層而為四，至於九自乘八十一，則其羃積亦合自一至十七九層之數而為八十一，皆以本數自乘而每形之冪積如之，得加乘之法則減除在其中矣。自此而衍之，至於無窮，其數無不合焉。推之九章之術，其理無不貫焉。今考洛書，縱横逆順，無往不得，加減乘除之法，開方句股之算，乃自其未變之先，而諸法渾具，至洛書而始盡其參伍錯綜之致云爾。
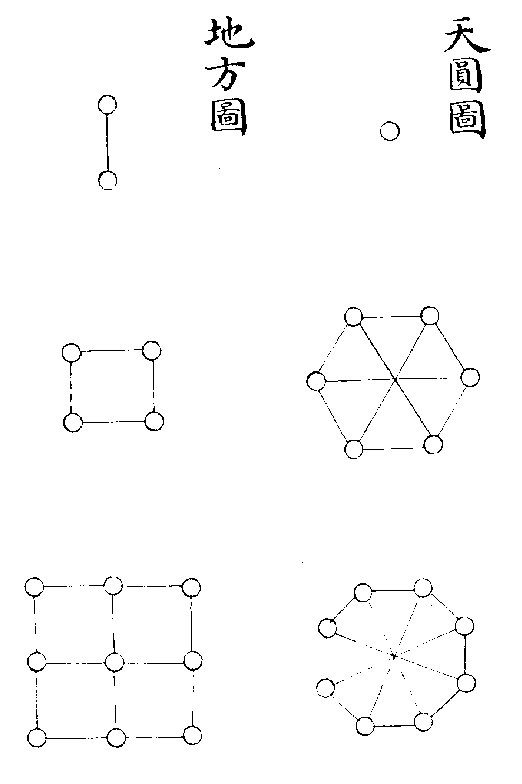
圖形合《洛書》為象法之原
天圓圖／地方圖
人為天地心圖
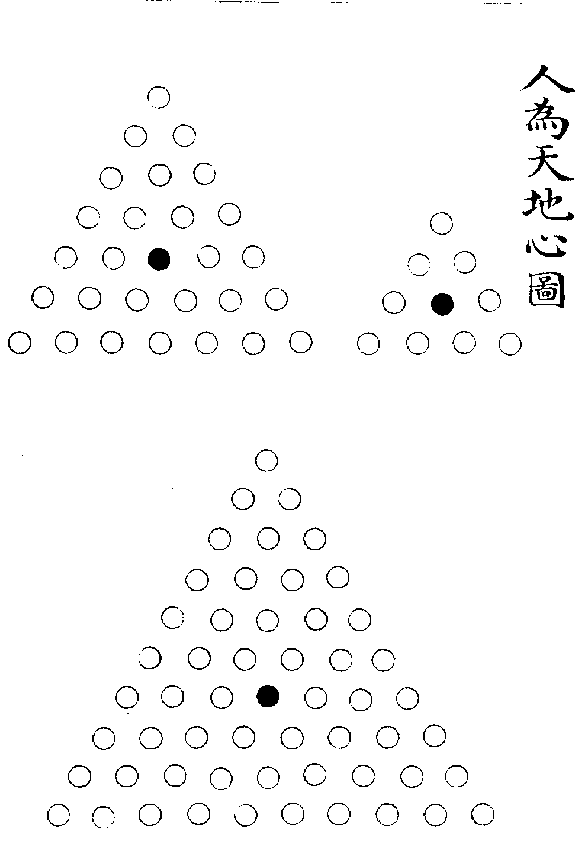
凡有數則有象，象不離乎數也。萬象起於方圓，而測方圓者以三角，此句股所以為算之宗也。圓者天象，方者地象，三角形者人象，何則？天之道如環無端，故其象圓也。地之道奠定有常，故其象方也。人受性於天，受形於地，猶三角之形，其心則圓之心，其邊則方之邊也。今就九數而三分之，則一者圓之根也，而十數之內，惟六角八角，為有法之圓形，其自十以後，角愈多以至於無角者視此矣，此一六八所以為圓象之數也。二者方之根也，而十數之内，惟四與九可以積成方面。其自十以後，積愈多而皆可成方者，視此矣。此二四九所以為方形之數也。以十數裁為三角，自一至四，則三其心也。自一至七，則五其心也。自一至十，則七其心也。所謂三角求心之法者如是，其自十以後，數愈多而皆可以求心者，視此矣。此三五七所以為三角形之數也。洛書之位，一六八居下為天道之下濟，二四九居上為地道之上行，三五七居中為人道之中處。其數其象，亦於圖形乎有合矣。
先後天陰陽卦圖
先天之陽卦曰震離兌乾，其陰卦曰巽坎艮坤。後天之陽卦曰乾震坎艮，其陰卦曰坤巽離兌，不同何也？蓋先天分陰陽卦，自兩儀而分之，由陽儀以生者，皆陽卦也；由陰儀以生者，皆陰卦也。後天分陰陽卦，自爻畫以定之，其以陽為主者，皆陽卦也；其以陰為主者，皆陰卦也。先天則因乎畫卦之序而中分之，後天則卦之已成，觀其爻畫之多寡而命之也。
其理如何？曰：陽儀上有陰卦，此所謂「立天之道曰陰與陽」也。陰儀上有陽卦，此所謂「立地之道曰柔與剛」也。
其法象之自然者如何？曰：火之炎熱光明，其為陽也，明矣。澤者水之積濕，為陽氣所驅，以滋潤萬物者也，是亦陽也。水之幽暗寒肅，其為陰也，明矣。山者土之隆起，與地為一體者也，是亦陰也。是故先天之卦，陰陽之象之正也。其變而後天，則火與澤從風而俱為陰，水與山從雷而俱為陽，蓋有由矣。凡陰陽之氣，未有不合而成者也，然有感應先後之別焉。先有陽而遇陰者屬陽，先有陰而遇陽者屬陰，有陽氣在下將發而遇陰壓之，則奮而為雷矣。有陽氣在中將散而遇陰包之，則鬱而為雨矣。有陽氣直騰而上而遇陰承之，則止而為山矣。此皆主於陽而遇陰，所以皆為陽卦也。有陰在內，陽氣必入而散之，觀之陰霾盡而後風息可見也。有陰在中，陽氣必附而散之，觀之薪芻盡而後火滅可見也。有陰在外，陽氣必敷而散之，觀之濕潤盡而後澤竭可見也。此皆主於陰而遇陽，所以皆為陰卦也。總而淪之，惟乾純陽，坤純陰，不可變也。雷陽動之始，風陰生之始，亦不可變也。火溫煖，澤發散，故以用言之則陽，然火根於陰之燥，澤根於陰之濕，故以體言之則陰。水寒涼，山凝固，故以用言之則陰，然水根於陽之噓而流，山根於陽之矗而起，故以體言之則陽。先天之象，著其用也。後天之象，探其根也。正如仁之發生為陽，而其柔和亦可以為陰。義之收斂為陰，而其剛決亦可以為陽。陰陽本一氣而互根，故其理竝行而不悖也。
後天卦以天地水火為體用圖
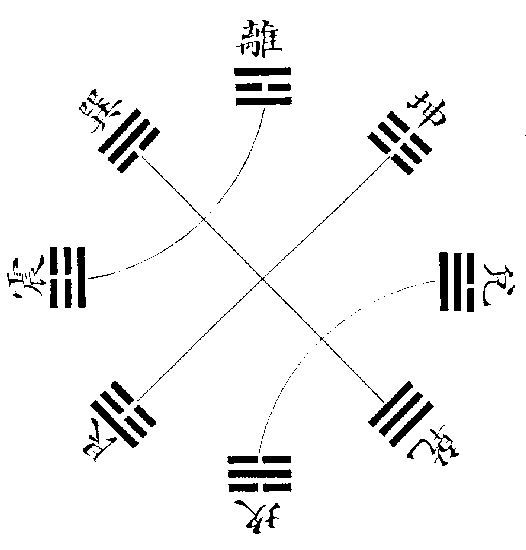
造化所以為造化者，天地水火而已矣。易卦雖有八而實惟四，何則？風即天氣之吹噓而下交於地者也，山即地形之隆起而上交於天者也，雷即火之鬱於地中而搏擊奮發者也，澤即水之聚於地上而布散滋潤者也。道家言天地日月，釋氏言地水火風，西人言水火土氣，可見造化之不離乎四物也。故先天以南北為經，而天地居之體也。以東西為緯，而水火居之用也。後天則以天地為體，而居四維。以水火為用，而居四正。雷者火之方發，故動於春；及火播其氣，則王於夏矣。澤者水之未收，故散於秋；及水歸其根，則王於冬矣。水火為天地之用，故居四正以司時令也。天氣朕兆於西北，至東南而下交於地，易所謂天下有風姤也。故乾巽相對而為天綱。地功致役於西南，至東北而上交於天，易所謂天在山中大畜也。故坤艮相對而為地紀。天地為水火之體，故居四維以運樞軸也。天地水火，體用互根，以生成萬物，此先後天之妙也。若以卦畫論之，則震即離也，一陰閉之於上則為震。兌即坎也，一陽敷之於下則為兌。巽即乾也，一陰行於下則為巽。艮即坤也，一陽亘於上則為艮。是以六十四卦始乾坤，中坎離，而終於既濟末濟。則知造化之道，天地水火盡之矣。
先天卦變後天卦圖
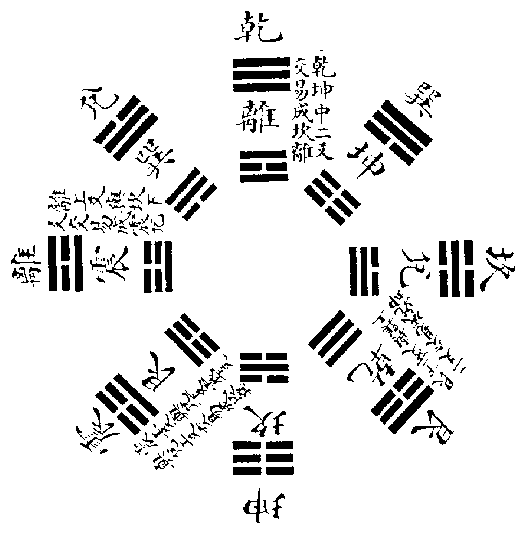
此圖先天凡四變而為後天也，蓋火之體陰也，其用則陽，而天用之，故乾中畫與坤交而變為離。水之體陽也，其用則陰，而地用之，故坤中畫與乾交而變為坎。火在地中，陰氣自上壓之而奮出，則雷之動也，故離上畫與坎交而變為震。水聚地上，陽氣自下敷之而滋潤，則澤之說也，故坎下畫與離交而變為兌。陽感於陰則山出雲，是山者雷與澤之上下相感者也，故震以上下畫與兌交而變為艮。陰感於陽而水生風，是風者澤與雷之上下相感者也，故兌以上下畫與震交而變為巽，風本天氣也，因與山交而入其下，則下與地接，故巽以上二爻與艮下二爻交而變為坤。山本地質也，因與風交而出其上，則上與天接，故艮以下二爻與巽上二爻交而變為乾。
或曰：此於經書有徴乎？曰：在易，天與火同人是天以火為用也，水與地比是地以水為用也。離為火亦為電，易曰雷電合而章，又曰雷電皆至，是雷與火一氣也。澤有水則為節，澤无水則為困，是澤與水一物也。《周禮》云「日西則多陰」，蓋西方積山，故多雲雷，今之近嶂者皆然也。又云「日東則多風」，蓋東方積澤，故多風颶，今之濱海者皆然也。莊周云「大塊噫氣，其名為風」，是風與地氣相接也。《禮》登山以祭，升中於天，是山與天氣相接也。夫天地水火者，一陰一陽而已，其情則交易而相通，其體則變易而無定，故先天交變以成後天，莫不各得其位而妙其化，各從其類而歸其根也。豈偶然哉！
先天卦配河圖之象圖
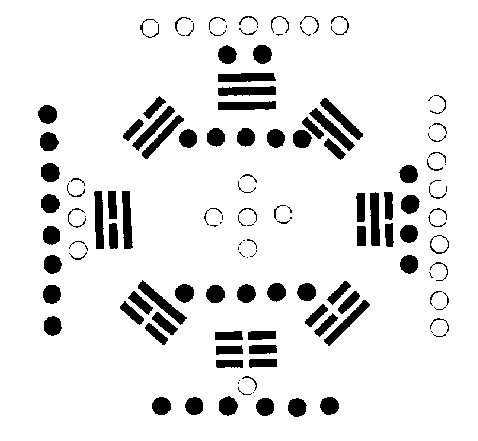
圖之左方，陽內陰外，即先天之震離兌乾，陽長而陰消也。其右方，陰內陽外，即先天之巽坎艮坤，陰長而陽消也，蓋所以象二氣之交運也。
後天卦配河圖之象圖
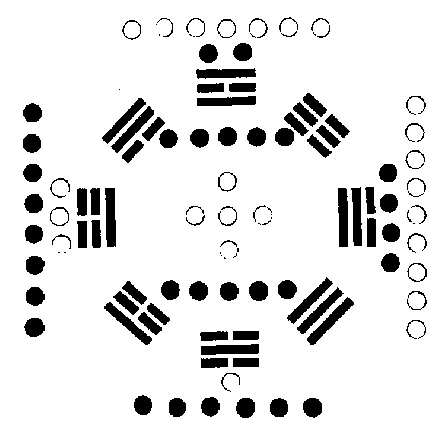
圖之一六為水居北，即後天之坎位也。三八為木居東，即後天震巽之位也。二七為火居南，即後天之離位也。四九為金居西，即後天兌乾之位也。五十為土居中，即後天之坤艮，周流四季而偏旺於丑未之交也。蓋所以象五行之順布也。
先天卦配洛書之數圖
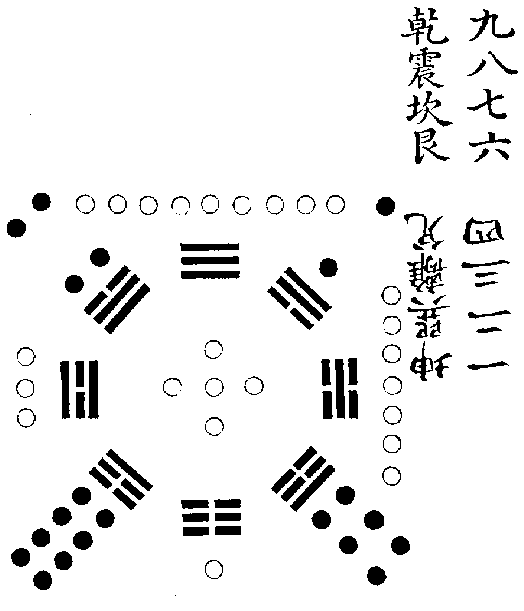
直列《洛書》九數，而虛其中五以配八卦。
陽上陰下，故九數為乾，一數為坤，因自九而逆數之，震八坎七艮六，乾生二陽也。又自一而順數之，巽二離三兌四，坤生三陰也。以八數與八卦相配，而先天之位合矣。
後天卦配洛書之數圖
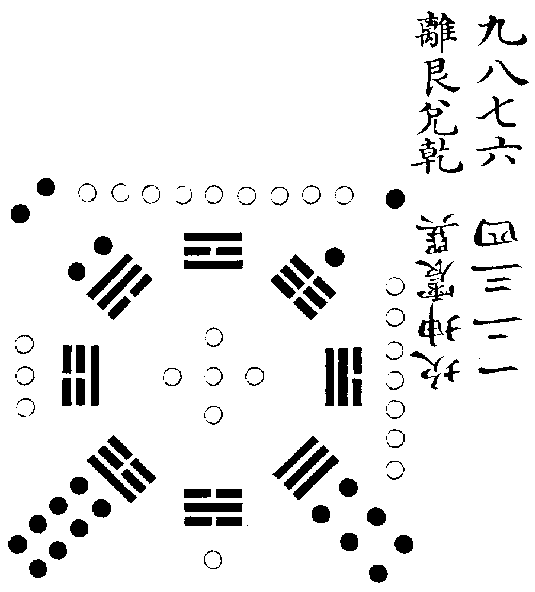
火上水下，故九數為離，一數為坎。火生燥土，故八次九而為艮。燥土生金，故七六次八而為兌為乾。水生濕土，故二次一而為坤。濕土生木，故三四次二而為震為巽。以八數與八卦相配，而後天之位合矣。
《洛書》之左邊，本一二三四也。其右邊，本九八七六也。然陰陽之道，丑未之位必交。《洛書》之二與八，正東北西南之維，丑未之位，此其所以互易也。以此類之，則先天圖之左方，坤巽離兌。其右方，乾震坎艮，以震巽互而成先天也。後天圖之左方，坎坤震巽。其右方，離艮兌乾，以艮坤互而成後天也。
據先儒說，圖書出有先後，又或謂並出於伏羲之世，然皆不必深辨。先聖後聖，其揆一也。況天地之理，雖更萬年，豈不合契哉。《洛書》晚出，而其理不妨已具於《河圖》之中，是故以易象推配，亦無往而不合也。
先後天卦生序卦雜卦圖說
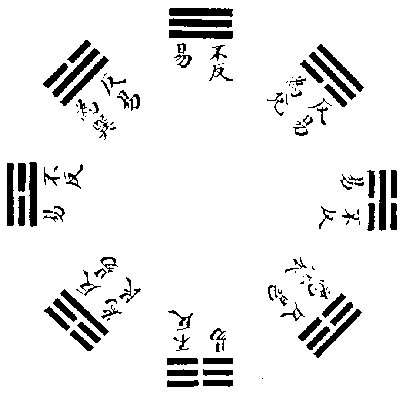
先天圖者，序卦之根也。
序卦之法，以兩卦相對為義，有相對而翻覆不可變者，乾坤、坎離、頤大過、中孚小過是也。有相對而翻覆可變者，屯蒙以後，既濟未濟以前，五十六卦皆是也。就五十六卦之中，則翻覆而二體不易者十二卦，需訟、師比、泰否、同人大有、晉明夷、既濟未濟也。翻覆而二體皆易者十二卦，隨蠱、咸恒、損益、震艮、漸歸妹、巽兌也。其翻覆而止於一體易者三十二卦，則自屯蒙至渙節皆是也。蓋翻覆而不可變者，法八卦之乾坤坎離也。翻覆而可變者，法八卦之震艮巽兌也。就翻覆可變之中，其二體不易者，又皆乾坤坎離相交者也。其一體不易者，亦皆交於乾坤坎離者也。惟震艮巽兌相交之卦，則二體皆易焉，頤、中孚、大過、小過。雖為震艮巽兌相交之卦，而翻覆不可變者，頤、中孚具離之象，大過、小過具坎之象也。故《序卦》以之附於坎離、既濟未濟，為其具離坎之象焉爾。
先天圖八卦兩兩相對，《序卦》之根也。乾與坤對，坎與離對，震與巽對，艮與兌對。相對而不相變，所以定《序卦》之體也。然既相對，則必相交。四正之卦相交，則雖翻覆，而其體不易。四維之卦相交，則翻覆而其體遂易矣。若四正之卦、與四維之卦雜交，則易者半，不易者半，所以極《序卦》之用也。是故天地定位，上經所以始於乾坤，中於否泰也。山澤通氣，雷風相薄，下經所以始於咸恒，中於損益也。水火不相射，上下經所以終於坎離、既濟未濟也。
艮☶ 下去一陰上生一陰則為坎
坎☵ 下去一陰上生一陰則為震
震☳ 下去一陽上生一陽復為艮
乾☰ 下去一陽上生一陽仍為乾
兌☱ 下去一陽上生一陽則為離
離☲ 下去一陽上生一陽則為巽
巽☴ 下去一陰上生一陰復為兌
坤☷ 下去一陰上生一陰仍為坤
艮☶ 下去一陰上生一陽為巽
坎☵ 下去一陰上生一陽為離
震☳ 下去一陽上生一陰為坤
乾☰ 下去一陽上生一陰為兌
兌☱ 上去一陰下生一陽為乾
離☲ 上去一陽下生一陰為坎
巽☴ 上去一陽下生一陰為艮
坤☷ 上去一陰下生一陽為震
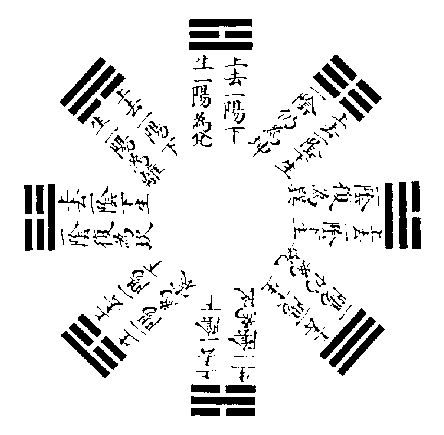
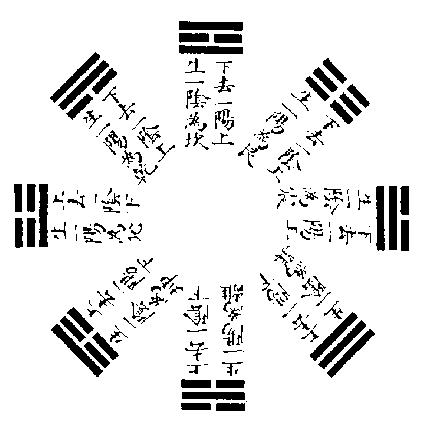
後天圖者，雜卦之根也。
雜卦即互卦也，互卦之法，或上去一畫而下生一畫，或下去一畫而上生一畫，則其體遂變矣。互體所成，凡十六卦，其陽卦從陽卦，陰卦從陰卦者八，乾坤，頤大過、蹇解、家人睽也。其陽卦交陰卦，陰卦交陽卦者亦八，剝復、夬姤、漸歸妹、既濟未濟也。以交互之法求之，乾而上去一陽，下生一陽，或下去一陽，上生一陽，仍是乾矣。坤而上去一陰，下生一陰，或下去一陰，上生一陰，仍是坤矣。惟震而上去一陰，下生一陰，則變為坎；下去一陽，上生一陽，則變為艮。巽而上去一陽，下生一陽，則變為離；下去一陰，上生一陰，則變為兌。坎而上去一陰，下生一陰，則變為艮；下去一陰，上生一陰，則變為震。離而上去一陽，下生一陽，則變為兌；下去一陽，上生一陽，則變為巽。艮而上去一陽，下生一陽，則變為震；下去一陰，上生一陰，則變為坎。兌而上去一陰，下生一陰，則變為巽。下去一陽，上生一陽，則變為離。此八變者，皆陽得陽卦，陰得陰卦，故乾之變則乾也，坤之變則坤也。震之變則雷水解也，山雷頤也。巽之變則風火家人也，澤風大過也。坎之變則水山蹇也，雷水解也。離之變則火澤睽也，風火家人也。艮之變則山雷頤也，水山蹇也。兌之變則澤風大過也，火澤睽也。皆因其能相變，故能相合也。又乾而上去一陽，下生一陰，則變為巽。下去一陽，上生一陰，則變為兌。坤而上去一陰，下生一陽，則變為震。下去一陰，上生一陽，則變為艮。震而上去一陰，下生一陽，則變為兌；下去一陽，上生一陰，則變為坤。巽而上去一陽，下生一陰，則變為艮；下去一陰，上生一陽，則變為乾。坎而上去一陰，下生一陽，或下去一陰，上生一陽，皆變為離。離而上去一陽，下生一陰，或下去一陽，上生一陰，皆變為坎。艮而上去一陽，下生一陰，則變為坤；下去一陰，上生一陽，則變為巽。兌而上去一陰，下生一陽，則變為乾；下去一陽，上生一陰，則變為震。此八變者，皆陽得陰卦，陰得陽卦。故乾之變則天風姤也，澤天夬也。坤之變則地雷復也，山地剥也。震之變則雷澤歸妹也，地雷復也。巽之變則風山漸也，天風姤也。坎之變則既濟也，未濟也。離之變則未濟也，既濟也。艮之變則山地剝也，風山漸也。兌之變則澤天夬也，雷澤歸妹也。亦皆因其能相變，故能相合也。易互卦之法盡於此，此其卦所以止於十六也。
後天圖八卦陰陽上下畫互變，雜卦之根也。何則？後天之卦，有各從其類以相變者焉，有各得其對以相變者焉。乾居西北，而三陽從之。坤居西南，而三陰從之，此各從其類者也。乾與巽對，坎與離對，艮與坤對，震與兌對，此各得其對者也。相從者除乾坤純陽純陰不變外，坎而上去一陰，下生一陰，則為艮。艮而上去一陽，下生一陽，則為震。震而上去一陰，下生一陰，則復為坎，此三陽相次之序也。巽而上去一一陽，下生一陽，則為離。離而上去一陽，下生一陽，則為兌。兌而上去一陰，下生一陰，則復為巽，此三陰相次之序也。相對者，乾而上去一陽，下生一陰，則為巽。坎而上去一陰，下生一陽，則為離。艮而上去一陽，下生一陰，則為坤。震而上去一陰，下生一陽，則為兌。此四陽卦變為對位四陰卦之序也。巽而下去一陰，上生一陽，則為乾。離而下去一陽，上生一陰，則為坎。坤而下去一陰，上生一陽，則為艮。兌而下去一陽，上生一陰，則為震。此四陰卦變為對位四陽卦之序也。然尋其對位相變之根，則又自父母男女長少而來，蓋四陰卦，兌為最少，離為中，巽為長，坤為老。四陽卦，艮為最少，坎為中，震為長，乾為老。凡變者自少而老。故兌而上去一陰，下生一陽，則變為乾矣。離而上去一陽，下生一陰，則變為坎矣。巽而上去一陽，下生一陰，則變為艮矣。坤而上去一陰，下生一陽，則變為震矣。四陽卦之變，自陰而來，故又變而為對位之四陰也。艮而下去一陰，上生一陽，則變為巽矣。坎而下去一陰，上生一陽，則變為離矣。震而下去一陽，上生一陰，則變為坤矣。乾而下去一陽，上生一陰，則變為兌矣。四陰卦之變，自陽而來，故又變而為對位之四陽也。
合而觀之，凡陽卦相變者，震變坎艮也，坎變震艮也，艮又變震坎也。凡陰卦相變者，巽變離兌也，離變巽兌也，兌又變巽離也。凡陽卦變陰卦者，乾變巽兌也，震變坤兌也，坎變離也，艮變坤巽也。凡陰卦變陽卦者，坤變震艮也，巽變乾艮也，離變坎也，兌變乾震也。易中所謂互卦者止於此，而其錯綜次序，皆具於後天也。
大衍圓方之原
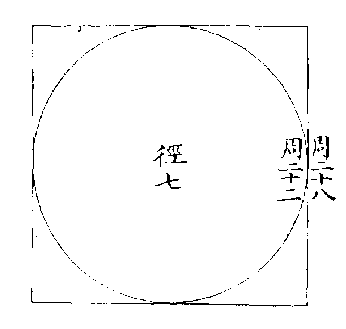
凡方圓可為比例，惟徑七者。方周二十八，圓周二十二，即兩積相比例之率也。（用其半，故若十四與十一。）合二十八與二十二，共五十，是大衍之數，函方圓同徑兩周數。
大衍句股之原
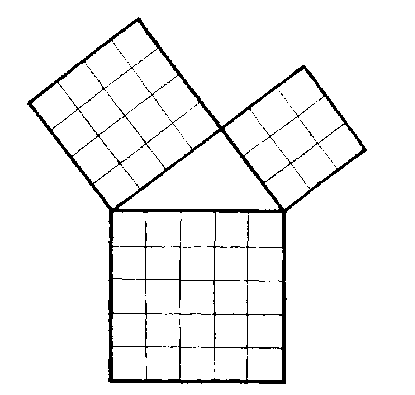
句三，其積九。
股四，其積十六。
弦五，其積二十五。
合之五十，是大衍之數，函句股弦三面積。
蓍策之數，必以七為用者，蓋方圓之形，惟以徑七為率，則能得周圍之整數。句股之形，亦惟以三四為率，則能得斜弦之整數。徑七，固七也。句三股四之合亦七也。是故論方圓周圍之合數則五十，論句股弦之合積亦五十，此大衍之體也。因而開方，則不盡一數。而止於四十九，此大衍之用也。開方而不盡一數，則蓍策之虛一者是已。方面之中，函八句股，而又不盡一數，則蓍策之掛一者是已。惟老陽老陰之數，與此密合，故作圖以明之。
老陽數合方法
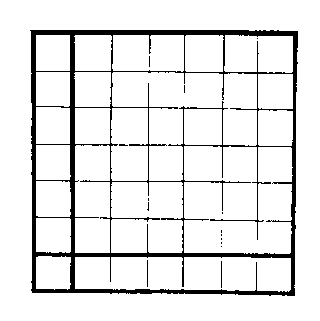
全方四十九。
中含大方六六三十六，為過揲之數。
小角一一如一，一六五互乘為十二，併成十三，為掛扐之數。
此與前《洛書》以自乘互乘為積方之法同，但《洛書》用對數，如一與九之類是也。大衍用合數，則一與六是也。
老陰數合句股法全方四十九。
老陰數合句股法
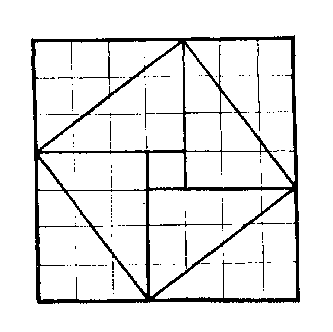
全方四十九。
句三股四，其積六，四因之得二十四，為過揲之數。
弦五，其積二十五，為掛扐之數。（弦實亦函四句股積，而多句股較一。）
十數之中，除一一不變，自二二至十十，皆可成方。然惟三三則五數居其中，七七則二十五數居其中，此二者為能得天地之中數，餘則不能也。蓋三二者《洛書》之數也，七七者蓍策之數也。《洛書》之數，五居其中矣，而其四方，則又成四句股之數，而以中五為弦之法焉。蓍策之數，二十五居其中矣，而其四方、則又具四句股之積而即以二十五為弦之實焉。是故卦數之八，合乎《河圖》之四也，為其虛五十者同一根也。蓍數之七，合乎《洛書》之三也，為其用中五者同一根也。聖人因心之作，與天地自然之文，其相為經緯者如此。
大衍迎日推策法
史稱黃帝迎日推策。所謂策者，蓋即神蓍也。推衍策數以候日月，故曰「迎日推策」。
考之後代，譚卦畫者多以曆法推配，然孔子未嘗言也，惟於大衍之數則曰「象四時」「象閏」，又曰「當期之日」，則蓍策之與曆法相表裏也，可見矣。顧有以理言之而肖似者，有以數推之而密合者。以理言而肖似者，孔子《大傳》所陳是也。蓋四十九算，排列成方，以句股之數求之，則零一者歸於中而為心；以開方之法求之，則零一者歸於隅而為角。以其歸於中也，故分二以象天地，而掛一者象人之為天地心也。以其歸於隅也，故分二以象二氣，而掛一者象閏之為一歲，餘也，大傳所謂掛一以象三者。此零一之策也，所謂歸奇於扐以象閏者亦此零一之策也。然當分二之初，此一之掛者，徒以象氣盈耳。至於每揲之後，又得餘策而扐之，然後以此掛一者歸之，而并以象閏，則合氣盈朔，虚而為一者也。此以理言之，而大概相似，是孔子之說也。至於以數推之者，自黄帝之法不傳，至唐僧一行始以大衍命曆以策數起歲，分閏餘之算。然按《唐書‧曆志》考之，其法蓋未密合也，故今以孔子之言為宗，而參以一行之數，康節之理，據顓頊周髀之制，以約略千載坐致之術為法，表以眀之如左：
一年三百六十五日四分日之一。每日百分。凡三萬六千五百二十五分。以天數二十五除之，得一千四百六十一分，為日數。又以地數三十除日數，得四十八零七分，為月數。是為大衍用數。
《大傳》言蓍數，而以《河圖》之數首之，故一年全數，以二十五除之得日數者。日有曉午昏夜，凡四限，四分期日，為一千四百六十一也；以三十除之得月數者，月有朔望，上下弦凡四限，四分歲月（每月三十日算），為四十八零七分也，與大衍用數相應。
揲策合左右共四十八，應四十八弦（每弦七日半），為期日歲月之經數（三百六十）。
掛策一，應氣盈之餘數（五日四分日之一）。
以初變為主。
日法十。
揲策應弦，每弦以十分為率。
掛策應氣盈五日四分日之一，於日法為十分弦之七。
扐策合陰陽共十二（得少則四為陽，得多則八為陰），應十二朔（每朔二十九日，九百四十分日之四百九十九），為一歲之實數（三百五十四日，九百四十分日之三百四十八）。
掛策一，應朔虛之餘數（十日九百四十分日之八百二十七）。
亦以初變為主。
月法十九。
扐策應朔，每朔以十九分為率。
掛策應朔虛十日九百四十分日之八百二十七，於月法為十九分朔之七。
以初變之揲策扐策計之，揲策四十八，以應四十八弦之整數，其掛一者以應氣盈五日四分口之一也。扐策十二，以應十二朔之實數。其掛一者，以應朔虛十日八百二十七分也。據四分曆法，每日九百四十分，故一歲之氣盈，有五日二百三十五分。一歲之朔虛（此合氣盈總算），有十日八百二十七分，每弦七日四百七十分，如日法十分弦之七，則為五日二百三十五分矣；每朔二十九日四百九十九分，如月法十九分朔之七，則為十日八百二十七分矣。（月每日行十二度十九分度之七，故以十，九為法），日月之法不同，而其餘分皆七。故漢儒卦氣，每卦直六日，尚餘七分。（每卦直六門七分者，日以八十分為法也。蓋歲數三百六十五日四分日之一，四乘而三除之，為四百八十七，故四百八十七者，歲策也。每卦直六日，六八四十八，得四百八十分，又餘七分，歲策之根也。積六十卦，直三百六十日，餘分之積，共四百二十分，以日法除之，為五日四分日之一。）古今曆法，一章之內，有七閏月者，法由茲起也。其在蓍數，則何以見掛一之策，為餘七之算乎？蓋亦以生蓍之法而知之爾。卦數八八者，體數也。蓍數七七者，用數也。蓍以七為用，而掛一者用中之用，故其分數亦止於七也。此皆以一行之曆，康節之說，參而用之者。然一行以弦為實弦，而不足七日有半，以掛一為實閏，而其數又餘於一弦之外，故今以弦為七日半之經，弦以掛一為五日四分日之一之盈分，必待扐餘之後，然後其歸奇之掛一，乃得應十日八百二十七分之數，而為一歲之實閏也。似於大傳之先後次序，更為脗合
過揲為正策（乾策三十六，合六爻二百一十有六。坤策二十四，合六爻百四十有四）。
凡三百有六十當一期之日數。
掛扐為餘策（乾策十三合六爻七十有八，坤策二十五合六爻百五十）。
凡二百二十有八，當一章之月數。（正策以三十為進退之法，故其合皆六十，餘策以十九為進退之法，故其合皆三十八，三十者，日法也，十九者，朔法也。）
二篇之策為全策。（陽爻百九十二，得六千九百一十二，陰爻百九十二，得四千六百零八。）
凡萬有一千五百二十，當閏終之總數。
此因《大傳》之說而推備之者。歲者，正數也，太陽主之；閏者，餘數也，太陰主之。故《堯典》始而殷正四時，則曰日中、日永、日短，此以太陽為主者也，終則曰以閏月定四時成歲，此以太陰為主者也。蓍策之正數三百有六十，當一期之日，蓋日周天而為一期，故為太陽所主也。其餘數二百二十有八，當一章之月，蓋氣朔分齊而為一章，故為太陰所主也，其全數萬有一千五百二十，當閏終之總數，蓋三十二月而閏一月，其辰萬有一千五百二十；三十二年而閏一年，其日萬有一千五百二十。此則日月正餘會終，蓍卦齊同之數也。
歷代之曆，歲分消長不同，故有五日四分日之一而有餘者，亦有五日四分日之一而不足者，然舉其中者以該其變者，則四分為常法，故顓頊曆《周髀經》皆用之，而司馬遷曆書述焉，蓋古法也。
乾策坤策圖
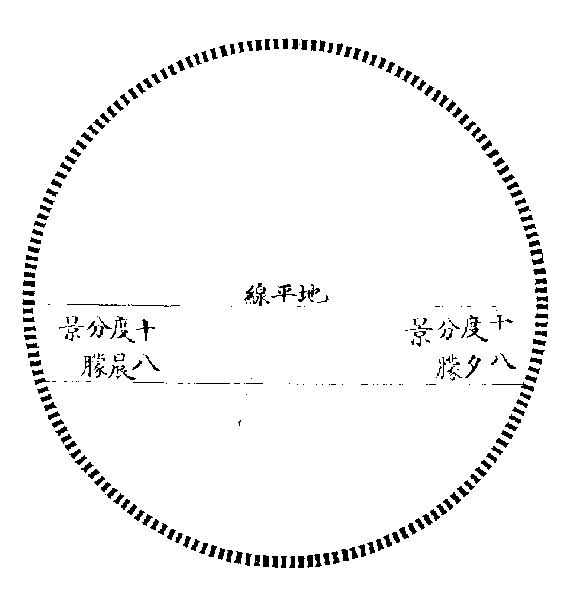
以地平線分周天之度為二，各一百八十度。日出入朦景昏旦各十八度，共三十六度，以加晝景一百八十度，合二百一十有六，則乾之策之數也。以減夜漏一百八十度，餘一百四十有四，則坤之策數也。
《大傳》曰：「乾坤之策，凡三百有六十，當期之日。」故各一百八十者，寒暑晝夜並行之體數也。然陽生而陰殺，陽明而陰暗，故陽饒而陰乏，陽盈而陰虛。今以晝夜平分推之，其自然之數如此，若一歲寒暑之候，則若邵子之說，開物於寅末，是亦先十八日也。閉物於戌初，是亦後十八日也。以故萬物之數，萬有一千五百二十，其從陽者六千九百一十二，其從陰者四千六百八，生氣常盛，則為豐年，善類常多，則為治世，其消息盈虛之理，亦若是而已矣。
加倍變法圖
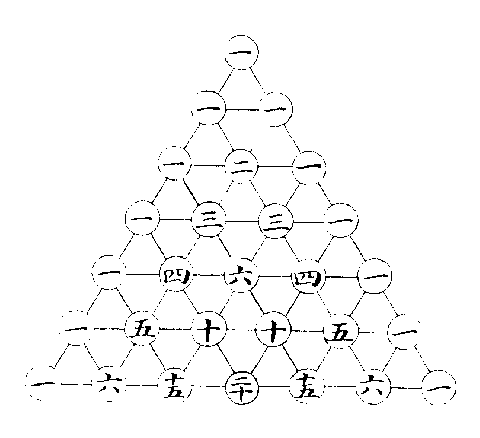
此圖用加一倍法。（如第二層兩一，生第三層中位之二，併左右兩一成四，是倍二為四也，第三層一二各生第四層中位之三，併左右兩一成八，是倍四為八也，下放此。）出於數學中，謂之開方求廉率，其法以左一為方，右一為隅，而中間之數，則其廉法也。（第三層為平方，第四層為立方，第五層六層七層，為三乘四乘五乘方。）於成卦之理，亦相肖合、伺則？陽大陰小，陽如方，陰如隅，分居兩端，陰陽合則生中間之兩象。如平方之方隅合而生兩廉，其長如方，其廣如隅也。又乘則生中間之六卦，如立方之方隅合而生六廉，三平廉根於方，而其厚如隅，二長廉根於隅，而其長如方也。故開方之法，雖相乘至於無窮，莫不依方隅以立算。成卦之法，雖相加至於無窮，莫不根陰陽以定體。成卦之始，一陰一陽，每每相加而已，及卦成而分析觀之，則自一畫至六畫，惟純陰純陽者常不動，其餘則方其為四象也，中間一陰一陽者二，方其為八卦也，中間一陰二陽者三，一陽二陰者三。方其為四畫也，中間一陰三陽者四，一陽三陰者四，二陰二陽者六。方其為五畫也，中間一陰四陽者五，一陽四陰者五，二陰三陽者十，二陽三陰者十。及其六畫之既成也，中間一陰五陽者六，一陽五陰者六，二陰四陽者十五，二陽四陰者十五，三陰三陽者二十。
朱子卦變之圖，以此而定也，蓋其倍法同於畫卦，而其多寡錯綜之數，則卦變用之。