高亨著有《周易筮法新考》一文,可在其《周易古經通說》或者是重刊版的《周易古經今注》中找到。該文為《周易》提出一種很特殊的變卦法與占斷法。
這種方法的特點在於「宜變之爻」的概念,只有宜變之爻剛好落在「可變之爻」時才會以爻辭來占解,否則就用卦辭。
雖然高亨是我非常敬重的學者,也經常引用他的說法,《周易古經今注》也是我很推薦的一本易經注解。但高亨所提的變卦法問題相當多,是讓我難以認同的。但近來似乎有越來越多人採用,因此不得不正視此法的問題。
原本「宜變之法」只是高亨為了解釋經典某些疑義的大膽假設,需要經過驗證之後才宜於實際採用到占斷上。但外界似乎沒有人去驗證過此法的問題,然後便直接大力採用。而使用者多數未完全依循高亨的規則,混雜了傳統方法,因此不但難以察覺其中問題,也違反了高亨當初設計此法旨在恢復周朝古法的初衷。
本文目的是要好好的驗證這個假設是否符合高亨所要證明的春秋筮例,還有占筮法的使用情境?
驗證結果發現,此法有以下問題,要採用之前請深思:
- 卦象的表達方式很混亂,所見非所得,所得非所見。
- 宜變之爻的發生位置,只固定發生在特定的兩、三爻上。
- 有些爻位的發生機率為零,例如乾卦初九不可能發生。
- 完全無法通過各種機率的驗證。機率上極度不合理,且完全與春秋筮例不符。
《周易筮法新考》的變卦與占法介紹
營數
這個占法的關鍵在於「宜變之爻」的概念,要了解宜變之爻要先了解營數。
高亨如此定義「營數」:
每卦六爻,每爻或「九」或「八」,或「七」或「六」,是謂四營,即不出於此四種營數也。
高亨所謂的「營數」就是揲蓍結果所得的六、七、八、九等四個筮數,每一爻都會有一個營數。因此六爻營數總和最少為 36(6x6),最多為 54(9x 6)。
例如,你得到的卦由下到上筮數分別是977, 777,這一卦的營數就是把六個數加起來,9+7+7+7+7+7 等於44。
營數概念出於《繫辭傳大衍章》「四營而成易,十有八變而成卦」。高亨所定義的「營」還有「四營」和荀爽一致,但這樣的理解個人不是很贊同。《大衍章》中的四營指的是分二、卦一、揲四、歸奇等四個步驟。四營而成易,易者變也。四個步驟就完成一「易」,也就是一「變」。每爻會有三變,所以一卦有18變(3x6),共72營。六、七、八、九應名為「筮數」較佳。我所持的這個看法,也是孔穎達、朱熹等先儒的看法。
天地之數
《繫辭大衍章》:「天數五,地數五,五位相得而各有合。天數二十有五,地數三十,凡天地之數,五十有五,此所以成變化,而行鬼神也。」這裡的天數五指的是 1, 3, 5, 7, 9 等五個奇數,地數五為 2, 4, 6, 8 10 五個偶數。天數為五個奇數相加為 25,地數為五個偶數相加為 30,天地之數就是 25 +30 =55。
高亨認為,55 這個天地之數必有其用,既然 50 與成卦之法有關,那麼 55 必然和變卦有關。具體來說, 55 是用來決定「宜變之爻」的,進一步決定之卦要如何畫卦。因為他發現到,這剛好與最大的營數 54 差 1。意思好像是說,六爻全是九時,初爻(1)就是宜變之爻。
不過六爻全是九時他認為是要用乾卦「用九」來解,這一點倒是和傳統無異。
可變之爻
就是得六或九之爻,而七與八則是不可變。
傳統理論原本認為該變的六和九,在高亨理論下都降級,變成只是「可以變」,但也可以不變。因為它還得剛好是「宜變之爻」才真的可以變;或者是在三個可變之爻以上時,可變之爻全都沒遇上宜變之爻,也要變。
宜變之爻
↓ 宜變之爻的推算。變數求法:55 - (六爻數字總和)
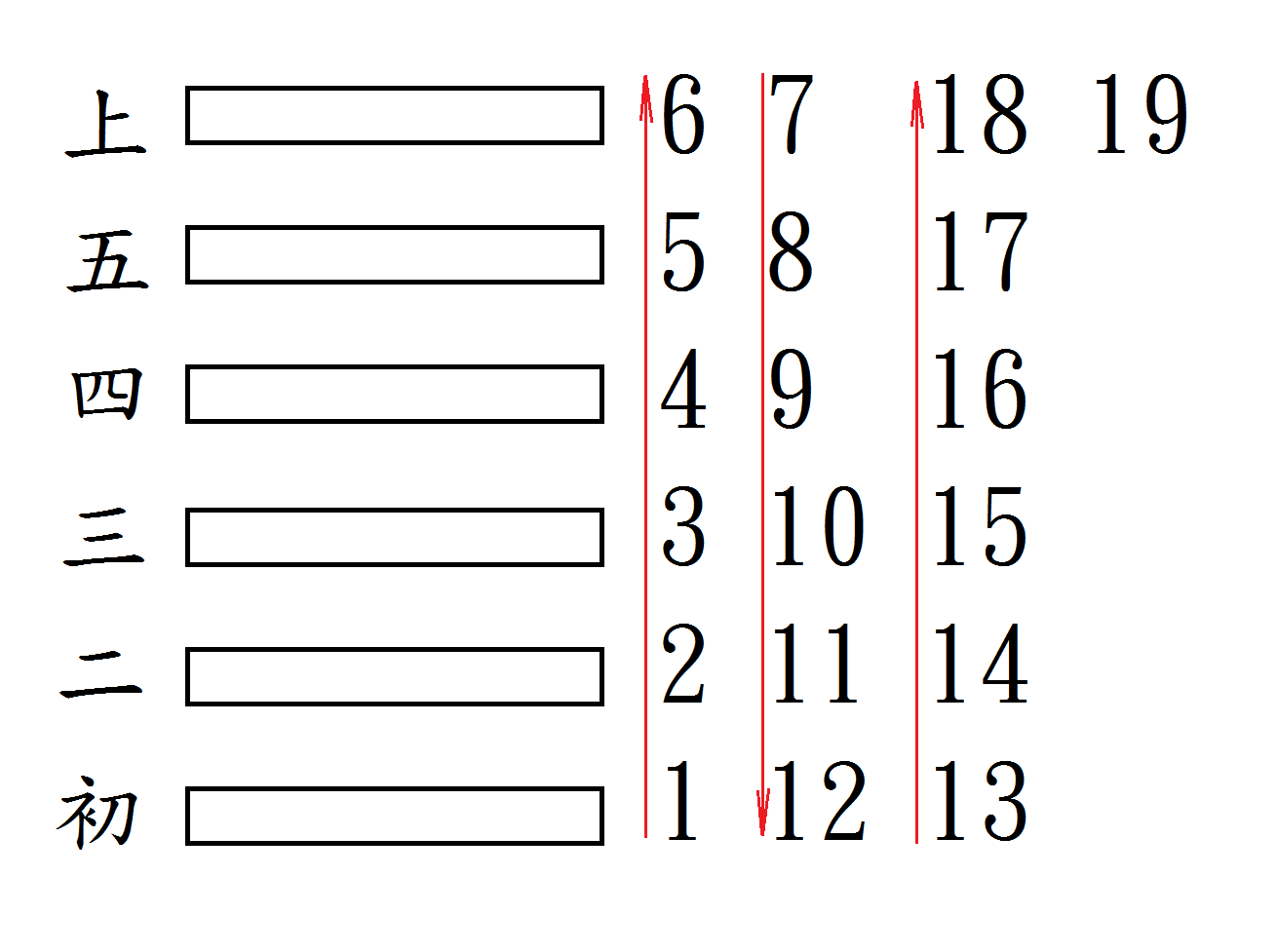
以天地之數 55 減去六爻營數可得數V,V這個數我姑且將它叫做「變數」。接著從初爻數到上爻,再從上爻數至初爻,再從初數至上,一直數到變數用盡為止(如上圖)。
例如,前面我們得到 9 7 7, 7 7 7(下至上),傳統會說是乾之姤。
但依高亨的方法,此卦營數是 44,所以變數就是 55-44 = 11。依上圖,乾卦九二才是宜變之爻,但此卦第二爻為七,所以這一卦應當以乾卦卦辭來占斷,而且應該說遇到了「乾之七」,不叫「乾之姤」。
但據我側面觀察,很多使用高亨之法的人這一卦會叫做乾之姤,然後再另外說明宜變之爻在第二爻。顯然並沒有完全依照高亨方法的規定在做。而且仔細研究高亨文章之後更可發現,高亨在「實徵」時,顯然也不熟悉他自己所設定的遊戲規則,完全不知這中間的變化與實用情境,造成他在實徵春秋筮例時荒腔走版。
事實上後文證明發現,依高亨的方法,絕對絕對不可能出現乾之姤這一卦。
高亨並提供一個表格對照,讓人可以「快速」查閱宜變之爻,有興趣的可以自己去翻他的書來看。這裡所提供的簡圖,是為便於速查宜變之爻而另外設計。由於六爻營數最小是36,55-36=19,所以表列只到19。
變卦法與占法
高亨所列占法相當的繁瑣,而且艱深難懂。所以這裡不詳述。有興趣的可以參考這裡,有人整理好了。
本文除了講重點概念,另外就是幫忙補充高亨沒講清楚的。
高亨占法的基本原則就是「可變之爻」要遇到「宜變之爻」時才算真的「變爻」,占解時就從本卦中去看此變爻。否則就是以卦辭來占解。
假設可變之爻很多時(例如三個或四個),可變之爻完全沒有宜變之爻,那麼可變之爻全變,改用之卦來占解。六變九,九變六。
但如果可變之爻有宜變之爻時該怎麼畫卦?照道理說,只有宜變之爻的陰陽要變,其餘可變之爻都不能變。
例如,你得卦777999(由下而上),55-48 = 7,所以這一卦的宜變之爻為乾卦上九,畫出的卦是乾之夬,不是乾之泰。
但反過來,當你看到乾之夬時,你會發現到所得到的數絕對不會是777779,而是可能你原本認為的乾之泰,但也可能並不是,因為三個9會落在那三爻你也不知道。而且,基本上此法不可能會出現乾之泰這種卦。
而你以為得到乾之夬時其實是乾之七而不是乾之夬,因為777779這個卦的宜變之爻在二。其六爻營數為44,所以變數為55-44=11,所以宜變之爻在二,但此卦的二位得到的營數是七,所以依高亨之法其實是要叫做「乾之七」。然而,再反過來想,當你看到乾之七時,實際上你不可能知道七是在那個位置,9又是在那個位置,有多少個9,多少個7也不知道。
我們再簡單說一下上面的情況:你以為的乾之泰在高亨占法裡其實叫乾之夬,而且其實不可能有乾之泰。你看到的乾之夬在高亨占法裡要叫做乾之七,但當你看到乾之七時,它又不見得是你以為的乾之夬,而且基本上如果沒有把原始筮數畫給你看,你完全無法反推出乾之七的卦象。
看到這裡,你有感覺到一種卦不卦,爻不爻的混淆了嗎?
高亨此法造成的「亂象」,卦象變得非常混亂而難以溝通。完全所見非所得,所得非所見!
這個問題雖然很顯著,但應用者通常沒有遵照高亨的方法學,所以就不知道有這個狀況。通常大家其實都是混搭傳統的卦象表現法,然後再另外推理宜變之爻。殊不知,這樣就違反了高亨想要解釋春秋筮例中諸如「艮之八」、「泰之八」這些卦例的苦心了。高亨此法設計既然號稱恢復周朝古法,那麼大家在應用時,就應當遵守他的遊戲規則來使用。應用者只要有遵守他的遊戲規則來做,很容易就會發現到這種卦象表達很混亂的嚴重問題。
但更嚴重的問題還在後面。
之卦使用時機
如果可變之爻超過三個(包括三個),然後可變之爻又沒有任何宜變之爻時,就得看之卦。這時候卦象的畫法是全部可變之爻都要變,然後以爻變之後的之卦來占解。
例如997999這一卦,有五個可變之爻,他的變數是55-52=3,所以宜變之爻是三,但三的位置是7不是可變之爻,所以這一卦就要以之卦來解了。這時候可變之爻才可全部九變六,六變九,所以這一卦就是乾之謙,並且要以謙卦來占解。
但假設這一卦是979,999,三既是可變之爻也是宜變之爻,那麼要改以九三來解釋,所以這一卦就變成是乾之履,看乾卦九三,並不是一般人認為的乾之師。
問題點
此法的問題相當多,無法一一詳舉。
在《周易筮法新考》後半,高亨列有〈東周筮法之實徵〉一個章節,但其實只是把卦例條列出來,故事簡單說明一下而已。多數卦例是什麼也沒徵,少數只是很粗略說明。
接下來我們會好好幫忙做「實徵」的事。
前文中已經可看到,這個方法基本上會讓整個卦象的表達變得很繁瑣與困難,卦象的基本溝通與表達將出現問題。揲蓍結果與卦象之間的關聯原本是很直覺的,用了此法變成障礙重重。看到的得到的卦象經常無法反推到原始的筮數結果,而筮數也無法很直覺的產生卦象,必需經過一套艱深難懂的演算法。因此一定會造成占筮上的滯礙難行。
只是一般人在使用高亨方法時並沒有遵守他的遊戲規則,所以難以看到這些嚴重問題。
以下則要進一步深入來驗證其內在的問題。
乾無初,坤無上
這種占法將造成每一卦都只固定得到特定兩、三個爻位為宜變之爻的情況,其餘爻位就很難成為變爻。
而在最極端的情況下,有些爻辭不可能出現,就是機率為零。例如,乾卦無法有初九,坤卦無法有上六的情況。
先看乾卦。本卦為乾的所有可能營數組合,以及這些組合該如何占解,我們依變爻數詳列於下。
| 可變爻數 | 9x | 7x | 營數和 | 變數 | 占解 |
| 0 | 0 | 6 | 42 | 13 | 卦辭 |
| 1 | 1 | 5 | 44 | 11 | 九二or乾卦辭 |
| 2 | 2 | 4 | 46 | 9 | 九四or乾卦辭 |
| 3 | 3 | 3 | 48 | 7 | 上九or某卦辭 |
| 4 | 4 | 2 | 50 | 5 | 九五or某卦辭 |
| 5 | 5 | 1 | 52 | 3 | 九三or某卦辭 |
| 6 | 6 | 0 | 54 | 1 | 用九 |
如上所列,上表已能把本卦為乾的所有狀況都包含進去。
如果你得到的是一個可變之爻,只有九二爻可以變,就是只有乾之同人時才是乾之同人,基本上不可能有什麼乾之姤、乾之履、乾之小畜,乾之大有、乾之夬的卦。
而如果是兩個可變之爻時,就只可能得到九四爻變。如果是三個變爻時,就只有上九可變。
以上三種變爻,占了絕大多數的比例,大約是96%。
所以,乾卦如果有變爻的話,幾乎都只固定在九二、九四,和上九,要得到九五的機會很小,而得到九三的機會極為渺茫,得到初九的機會是絕對不可能,就是零。
所以你可以把《周易》中初九潛龍勿用的經文撕掉了。
但還沒結束,多餘而用不到的經文還有。
同樣的狀況也會發生在坤卦,如下:
| 可變爻數 | 6x | 8x | 營數和 | 變數 | 占解 |
| 0 | 0 | 6 | 48 | 7 | 卦辭 |
| 1 | 1 | 5 | 46 | 9 | 六四or坤卦辭 |
| 2 | 2 | 4 | 44 | 11 | 六二or坤卦辭 |
| 3 | 3 | 3 | 42 | 13 | 初六or某卦辭 |
| 4 | 4 | 2 | 40 | 15 | 六三or某卦辭 |
| 5 | 5 | 1 | 38 | 17 | 六五or某卦辭 |
| 6 | 6 | 0 | 36 | 19 | 用六 |
如上所列,上表已能把本卦為坤的所有狀況都包含進去。
除了變爻多數只會發生在六四、六二之外,得坤卦上六的機會是零,所以《周易》也不需要坤卦上六龍戰於野的經文。
恭喜你,又可以少讀一段經文了。
接著我們再來抽驗其他類型的卦。
泰卦
絕大多數只能三、四、上爻變。
在泰卦的情況下,當可變之爻只有一個時,也就是一個九或一個六的時候,可變之爻不可能遇上宜變之爻,所以不可能有變爻。必需出現兩個可變之爻時,才可遇到宜變之爻,而且固定只會出現在三、四、上。
換句話說,當用於實際應用時,你若得到泰卦,要遇上有變爻可用的機會特別少,而要得初、二、五等三個爻變,更是機會渺茫。
四個可變爻的機率最高!
你沒看錯!
原本照道理來說,依揲蓍法的機率,應該是一個可變之爻的機率最高,其次是二個可變之爻,然後是沒有變爻,而且這三類應該超過八成。至四個可變之爻,機率已非常的低。
但是依高亨此法來統計春秋筮例,可能是四個可變之爻的卦例機率最高,這顯然是極為不合理的概率。
春秋筮例指的是《左傳》與《國語》中提到與《周易》解卦有關的故事,總共有21個故事,但其中有5個只是引述周易在講道理,並不是真實起卦的占解。因此與實際占例有關的故事有16個,其中有一個故事有兩卦,所以總共有17個卦例可供研究。
如前所述,依高亨的變卦法,卦象所見非所得,所得非所見,所以很多卦象都還得反推才能夠知道「可變之爻」的大致情況,例如到底有幾個可變之爻?但不見得可以精準反推出可變之爻。
我們就以其中數量最多的十個一爻變卦例來反推這些卦是什麼狀況(案:這裡所謂的一爻變,是依照傳統看法來看,若依照高亨占法,這些卦例不見得是一爻變)。
先以田敬仲父親筮得觀之否為例,來看一下我的計算方法。
首先驗證看這一卦是不是只有一個可變之爻,也就是一個六或九。
觀之否的宜變之爻落在觀卦六四,六四一定也是可變之爻。假設這一卦只有一個可變之爻,得到的營數由下到上應該是888677,六爻營數為44,變數為55-44=11,所以宜變之爻落在觀卦第二爻。依高亨占法的主張,這卦顯然不是888677。
但這一卦到底有幾個可變之爻才可讓六四爻既是宜變又可變?
我們比對一下表格發現,宜變之爻在六四的可能變數是4, 9, 16,與11最近而且相差是偶數的是9,比11少了2,所以六營爻數要46,也就是要再增2,只要再讓一個7變9,即可。
由於4和16與11的差都是奇數,所以不可能。
但兩個可變之爻只是其中某些可能,因為這還可能是四個可變之爻的例子。因為只要讓一個7 變為9,一個 8變為 6,同樣可以得到可變之爻落在六四。例如,886699,868699,以及688699依照高亨變卦法,也都是觀之否。
結論:這是一個兩個或四個「可變之爻」的卦例。若是二個可變之爻,為一六、一九,可能是888697(你原本以為的觀之晉),或888679(你以為的觀之萃)。若是四個可變之爻,為二六、二九,可能是886699,868699,以及688699。
我們依此法再詳推其他卦例,到底有幾個可變之爻?
全部結果表列如下:
- 觀之否 2或4個可變之爻
- 大有之乾 4個可變之爻
- 屯之比 4個可變之爻
- 屯之比 4個可變之爻
- 歸妹之睽 4個可變之爻
- 大有之睽 1或3個可變之爻
- 明夷之謙 4個可變之爻
- 困之大過 2或4個可變之爻
- 坤之比 5個可變之爻
- 泰之需 3個可變之爻
以上卦例高亨皆列於一個爻變(一個可變之爻)的卦例裡,並且說:「右十條皆以周易筮之者也,皆宜變之爻與可變之爻相值者也。」顯然高亨自己根本沒有好好實徵,沒有實際計算過宜變之爻如何落於可變之爻。因為實際上依他的理論去推算,只有大有之睽是一個爻變就有機會遇到宜變之爻,其餘根本都不是一個爻變的卦例。
我們再把春秋筮例中已知的其他三個及五個可變之爻的卦例算進去,並把一個不確定的泰之八扣除,三個以上宜變之爻的機率超過9/16,就是大約六成。
一個可變之爻的機率呢?
確定的是 0 個,而可能的只有1/17。但這照理說應該是機率最高的。
另一種機率算法
我們假定揲蓍過程當中,每個爻在產生時,為可變之爻的機率為1/4,不可變之爻的機率為3/4(這是依揲蓍法機率取概數,所以算是很可靠的數字,詳情可參考這篇文章)。
那麼以下是揲蓍取卦時得到各種變爻數可能的概略機率(不是精算):
| 可變之爻數 | 機率算式 | 機率 |
| 0 | (3/4)6 x (1/4)0 x1 | 729/4096 |
| 1 | (3/4)5 x (1/4)1 x6 | 1458/4096 |
| 2 | (3/4)4 x (1/4)2 x15 | 1215/4096 |
| 3 | (3/4)3 x (1/4)3 x20 | 540/4096 |
| 4 | (3/4)2 x (1/4)4 x15 | 135/4096 |
| 5 | (3/4)1 x (1/4)5 x6 | 18/4096 |
| 6 | (3/4)0 x (1/4)6 x1 | 1/4096 |
我們再加入「宜變之爻」的變數,計算出,當我們以揲蓍取卦時,最後以爻辭來占解的機率是多少?
- 一個可變之爻:(1458/4096) x (1/6) =5.9%
- 二個可變之爻:(1215/4096 ) x (2/6) =9.9%
- 三個可變之爻:(540/4096) x (3/6) =6.6%
- 四個可變之爻:(135/4096 ) x (4/6) =2.2%
- 五個可變之爻:(18/4096) x ( 5/6) =0.37%
總計 24.97 %
在解讀以上機率時要注意一下,這有點是鄉民說的「全世界平均每個人有一顆睪丸」的情況。事實上是男生有兩顆,女生零顆。以上機率是依總體情況來推算,但事實上就每一卦的情況來說會不盡相同,例如,前述泰卦一個可變之爻下以爻辭來占解的機率其實是零。
依上表,當你揲蓍時,得到四個可變之爻,然後宜變之爻剛好落在可變之爻的機率是2.2%!
但依高亨方法計算,這些已存筮例的機率卻有5/17~7/17,高達約3或4成的機率!顯示出這套理論與春秋筮例是完全不符的。
我們再把卦例限定在以爻辭來解釋的這十個來計算。以爻辭來占解的卦裡面,得一個至五個可變之爻的機率可推理如下:
- 一個可變之爻:5.9/ 24.97 = 23.6%
- 二個可變之爻:9.9/ 24.97 = 39.6%
- 三個可變之爻:6.6/ 24.97 = 26.4%
- 四個可變之爻:2.2/ 24.97 = 8.8%
- 五個可變之爻:0.36/ 24.97 =1.4%
我們假設春秋筮例採用的是高亨占法,那麼這十個卦例中,1-5個可變之爻的比例如下:
- 一個可變之爻:0或1/10
- 二個可變之爻:0或1/10或2/10
- 三個可變之爻:1/10或2/10
- 四個可變之爻:5/10或6/10或7/10
- 五個可變之爻:1/10
依照高亨占法的遊戲規則,照理說,如果以揲蓍法來起卦,最後你以爻辭來占解的卦例裡,可變之爻有一至三個的情況加起來應該是九成,一定會佔去一面倒的絕大多數,但實際上我們用高亨占法來推理春秋筮例,頂多只有4成是一至三個可變之爻,甚至可能低到1成。而四個可變之爻照道理說只有8.8%,10個裡面出現一個算剛好,兩個太多但可接受,三個的話還可勉強掰說無巧不成書,但這裡至少有5個,最多到7個,足足有一半之多。所以顯然春秋筮例所用的占法不可能是高亨所描繪的樣子。
「某卦之七」的卦例
依高亨的方法,如果可變之爻只有一或二個,但沒能用上時,卦象表達方法會看宜變之爻落在何處來表達卦象。例如,睽卦若宜變之爻落在第二爻,而筮得的卦第二爻是七,就會說「遇睽之七」。
你如果用揲蓍法,這類卦的出現機率會有多少?49.5%,大約是一半的機率。
- 一個可變之爻:(1458/4096) x (5/6) =29.7 %
- 二個可變之爻:(1215/4096 ) x (4/6) =19.8%
照理說看到一個或兩個可變之爻,然後以「某卦之七」或「某卦之八」來表達卦象並以卦辭來占解的例子應該會很多,17 個春秋筮例中照理說總計足足會有8個是得到一或兩個可變之爻且用「某卦之七」或「某卦之八」來占解。
我們總觀春秋筮例,總共有三個卦在表達卦象時使用到筮數,但都只使用了「八」,未用六、九,或七。甚至沒有我們現在諸如坤之六五這樣的表達方式。
- 重耳筮得晉國:得貞屯悔豫,皆八也。
- 董因筮重耳返晉:得泰之八。
- 穆姜筮出東宮:遇艮之八。史曰:是謂艮之隨。
是的,春秋筮例中沒有任何「某卦之七」的卦例!這樣的卦例是零!
只有一個「泰之八」的卦例類之,但這個卦是千古之謎,所以只能存疑,不能做真正的例證,它到底有幾個變爻正是有待證明的,不能做為證據來反證其他卦例。就算把它當做是高亨所認為的,是一或兩個可變之爻的卦例,但也只是1/17!
這三個卦例裡,泰之八所得筮數未詳之外,其餘兩卦都很清楚,一個是三個變爻,一個是五個變爻。因此可以歸納出,可能在多變爻的情況下,當時的人會用「八」來指涉是多變爻的情況,要改看卦,而不看變爻。
我們以穆姜的卦例來講,穆姜直接說是「艮之八」,可能原本他直接從本卦中看到多個變爻,原本以為要用艮卦來占解,所以說了艮之八。但由於這是多變爻的卦,應該看之卦,所以史官糾正說,是艮之隨,表示要看隨卦。
高亨則說:「非以余所言之變卦法,則此文...終末能解,亦可見余所言之變卦法非臆撰也。」但事實上,這個卦例是很好解的,並非如高亨說的無解。
從清華簡筮法的研就可清楚看出,《周易》之前的占筮法裡直接以數字為象,也就是所謂的「爻象」。爻象(數字)本身就有占斷吉凶的功能。但陰陽符號則要看卦象。比對周易可清楚看到與此類似的發展痕跡:七與八是陰陽符號,看的是卦象。而六與九則是類似帶有吉凶功能的占斷用數字,看的是爻象。所以周易占解的邏輯應該是得卦之後先看看有沒有六、九兩個數字,就以其所處爻來占解。若沒有,或過多,就改看卦。
公子親筮之,曰:「尚有晉國。」得貞屯、悔豫,皆八也。筮史占之,皆曰:「不吉。閉而不通,爻無為也。」
上面是重耳親筮是否可以得到晉國的卦,由於六、九有三個數,爻象已亂,沒有做為,要改看卦,所以筮史解釋説:「爻無為也。」爻沒有做為。所以只以卦來占解。
所以泰之八可能也是一個多變爻,然後必需改看卦的例子。因為該卦例只需看泰卦本卦,所以之卦是什麼?六、九在那些爻位?也不需講清楚。雖然我們無法反推該卦卦象,但應該就是一個多變爻的卦例。然後它以表達方式告訴你只需看卦象,不需看爻。
知道的我們講,不知道的就保留。但不要為了一個無法確認的事,將全部的占筮法給翻了過來。要提出新理論時,也要先做好精密的驗證。
高亨自己的暗中修正
或許高亨自己也隱隱覺得他這個占法的可能問題,所以其實他也在一個可變之爻的占法中很低調的加註一條:
又一爻為九六,亦可能不須求其宜變之爻,其為九即變為六,其為六即變為九,而得「之卦」,主要以本卦變爻爻辭占之。
所以,一個可變之爻時到底要怎麼占?這個說法又讓占法走回了傳統道路。如果這一條成立的話,那他講的那麼多「可變之爻」的理論做什麼用?做為多個可變之爻的備用?
事實上,外界在使用高亨此占法時,多數也都會忽略這個「可能」的例外使用狀況,因為這對於高亨的理論來說,並不具意義。這一條寫了其實反而亂上加亂,原本占法已夠亂了,現在又多了一條「可能」的例外法則,而怎麼例外法什麼也沒講。
這一條加注,最好的用途大概就是可以用來反擊我前面的機率計算。但是,只有承認此條的優先與合法性才能拿這一條來反擊我的計算,那麼也相當於承認宜變之爻就是胡扯瞎掰,大家其實應該改用這一段的占斷法。宜變之爻不用太在意。
所以,想引用這一條來抨擊我的機率計算的人,要請先大聲把這一段唸大聲一些,然後大聲說你認為要這樣占解才正確。但這也相當於否認了宜變之爻,並承認了我的主張。
事實上高亨在引用以上所列十個卦例時,他是認為那些卦都是可變之爻遇宜變之爻的。只是他沒有好好驗算,也沒發現那些卦例只有一個「有可能」是一個可變之爻就剛好遇上了宜變之爻(注意:是有可能,並不是確定)。
這就是紙上談兵的結果。
高亨只提理論,但自己並不占筮,所以實際用於占筮會有什麼狀況他自己甚至完全不知道。看到古書中表達卦象是一個變爻,就以為那是一個可變之爻,根本就不知道他的方法會造成所見非所得,所得非所見的混亂現象,依他的方法,所看到的卦象全部都是「假象」,不是真象。
《繫辭大衍章》的問題
高亨的這個方法除了沒有自己做好驗算之外,也有過度解讀《繫辭大衍章》及其價值的情況。
從很多面向來看,這可能是漢儒對於筮法的重建,但又加入了漢人的想法,應該不會是周代古法。
所以,這只是我們重建筮法不得不的選擇,因為也沒有其他資料可佐證了,只能先求有,再求精。等更多的出土資料來釐清更多疑問。
為什麼我說可能是漢人寫的?
- 一者,抄寫於漢文帝時代的長沙馬王堆出土帛書易傳裡,有《繫辭傳》,但裡面沒有大衍章,所以很可能是文帝之後才被收錄進去的。
- 二者,文字中充滿了對「五」這個數字的崇拜,和周易的九數崇拜,還有殘留的八數崇拜完全不一樣。所以較可能是戰國五行思想盛行之後所產生的,最早不會超過戰國時期。
- 三者,以春秋筮例的機率來反推,機率是不對的。但我們經修正,以48策來開始揲蓍,就與春秋筮例的機率完全一致。48之數就符合易經的數字崇拜,例如,此數中有8,且6爻x 8 純卦之數等於48。所以很可能是後人依當時方法湊到他們崇拜的50之數。
所以,面對《繫辭傳大衍章》,我們或許要多點懷疑,不宜當作聖經崇拜。而在做任何假設時,也不要過早下定論。更不要像先儒一樣,兩千年文人之精神全都空耗在這50-55的數字拳上了。或許等更多出土資料來印證時再做定論會較好。
高亨變卦法不可用!
這是本文簡單的結論。
以上我們只是就其理論本身的諸多弱點與不合理之處來談論。事實上,當代很多新出土資料可以釐清很多周易占筮法的基本問題,也可以與古法接軌。反觀,高亨的變卦理論,就目前的資料來看是完全格格不入,完全使不上力的。

高亨占解
之前沒真正看過高亨此篇文章,但確實見過同好使用,但不是用在一爻變,而是用在多爻變決定占斷的主爻。
如站長所述,一爻變占解法古來沒有太大爭議,更何況高亨提出的占解法沒有根據,在機率上也不合,高亨犯了學者常見的錯謬,一心只想證明自己對,從沒想過要試圖證明自己錯。
一爻變,沒有使用高亨此法的理由,我也沒有真正看人用過(可能想用的人都感受到站長說的矛盾點了吧?)。至於多爻變時,是否要用此法決定主爻?那可以留待同好自己判斷與驗證了。